Nad hipotenuzom  i katetama
i katetama 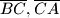 pravokutnog trokuta
pravokutnog trokuta  konstruirani su s vanjske strane kvadrati
konstruirani su s vanjske strane kvadrati 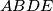 ,
, 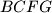 ,
, 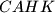 . Neka je
. Neka je  sjecište pravaca
sjecište pravaca 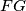 i
i 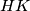 i neka su
i neka su  ,
,  ,
,  točke simetrične točkama
točke simetrične točkama  ,
,  ,
,  s obzirom na pravac
s obzirom na pravac  . Dokažite da točke
. Dokažite da točke  ,
,  ,
,  leže na pravcima
leže na pravcima 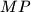 ,
, 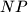 ,
, 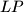 i da su trokuti
i da su trokuti  ,
, 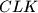 ,
, 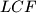 ,
, 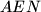 ,
, 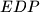 ,
, 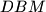 sukladni. Iscrtkajte te trokute! U kojem su odnosu peterokuti
sukladni. Iscrtkajte te trokute! U kojem su odnosu peterokuti 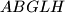 i
i 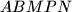 ? Što zaključujete promatranjem neiscrtkanih dijelova tih peterokuta?
? Što zaključujete promatranjem neiscrtkanih dijelova tih peterokuta?
 i katetama
i katetama 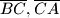 pravokutnog trokuta
pravokutnog trokuta  konstruirani su s vanjske strane kvadrati
konstruirani su s vanjske strane kvadrati 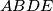 ,
, 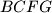 ,
, 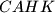 . Neka je
. Neka je  sjecište pravaca
sjecište pravaca 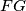 i
i 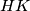 i neka su
i neka su  ,
,  ,
,  točke simetrične točkama
točke simetrične točkama  ,
,  ,
,  s obzirom na pravac
s obzirom na pravac  . Dokažite da točke
. Dokažite da točke  ,
,  ,
,  leže na pravcima
leže na pravcima 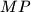 ,
, 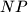 ,
, 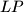 i da su trokuti
i da su trokuti  ,
, 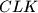 ,
, 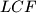 ,
, 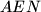 ,
, 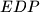 ,
, 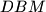 sukladni. Iscrtkajte te trokute! U kojem su odnosu peterokuti
sukladni. Iscrtkajte te trokute! U kojem su odnosu peterokuti 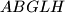 i
i 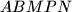 ? Što zaključujete promatranjem neiscrtkanih dijelova tih peterokuta?
? Što zaključujete promatranjem neiscrtkanih dijelova tih peterokuta?  Školjka
Školjka