Brojevi

su takvi da je
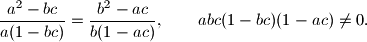
Ako je
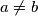
, dokažite da je
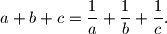
%V0
Brojevi $a, b, c$ su takvi da je $$
\frac{a^{2} - bc}{a(1 - bc)} = \frac{b^{2} - ac}{b(1 - ac)},\qquad
abc(1 - bc)(1 - ac) \neq 0.
$$
Ako je $a \neq b$, dokažite da je $$
a + b + c = \frac{1}{a} + \frac{1}{b} + \frac{1}{c}.
$$