Neka su

i

pozitivni realni brojevi takvi da je
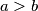
i
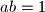
. Dokaži da tada vrijedi nejednakost
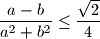
. Ako vrijedi jednakost, koliko je

?
%V0
Neka su $a$ i $b$ pozitivni realni brojevi takvi da je $a>b$ i $ab=1$. Dokaži da tada vrijedi nejednakost $\dfrac{a-b}{a^2+b^2} \leq \dfrac{\sqrt{2}}4$. Ako vrijedi jednakost, koliko je $a+b$?