U paralelogramu

točke

,

,

,

polovišta su stranica

,

,

,
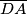
(tim redom). Pravci
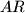
,

,
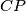
,
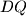
sijeku se i formiraju četverokut.

Dokaži da je taj četverokut paralelogram.

Nađi omjer površina tog i početnog paralelograma.
%V0
U paralelogramu $ABCD$ točke $P$, $Q$, $R$, $S$ polovišta su stranica $\overline{AB}$, $\overline{BC}$, $\overline{CD}$, $\overline{DA}$ (tim redom). Pravci $AR$, $BS$, $CP$, $DQ$ sijeku se i formiraju četverokut.
$a)$ Dokaži da je taj četverokut paralelogram.
$b)$ Nađi omjer površina tog i početnog paralelograma.