Slični zadaci
Za kupnju školskog autobusa koji će prevoziti djecu iz četiri mjesta  ,
,  ,
,  ,
,  potrebno je
potrebno je 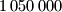 kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu
kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu  je stanovnika koliko u mjestima
je stanovnika koliko u mjestima  i
i  zajedno, u mjestu
zajedno, u mjestu  je
je 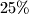 manje stanovnika nego u
manje stanovnika nego u  , a
, a 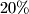 više nego u
više nego u  . Odredi kolike će iznose platiti pojedina mjesta.
. Odredi kolike će iznose platiti pojedina mjesta.
 ,
,  ,
,  ,
,  potrebno je
potrebno je 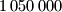 kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu
kn. Mjesta će snositi dio troškova srazmjerno broju stanovnika. U mjestu  je stanovnika koliko u mjestima
je stanovnika koliko u mjestima  i
i  zajedno, u mjestu
zajedno, u mjestu  je
je 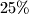 manje stanovnika nego u
manje stanovnika nego u  , a
, a 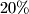 više nego u
više nego u  . Odredi kolike će iznose platiti pojedina mjesta.
. Odredi kolike će iznose platiti pojedina mjesta.  Školjka
Školjka 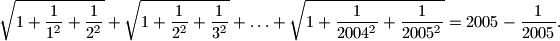
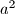 ,
, 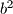 ,
, 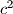 ako vrijedi jednakost
ako vrijedi jednakost 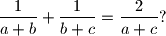
 su takvi da je
su takvi da je 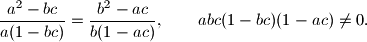
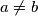 , dokažite da je
, dokažite da je 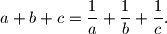
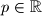 jednadžba
jednadžba 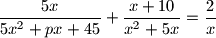 nema nijedno rješenje?
nema nijedno rješenje?  ,
,  ,
,  ako je
ako je 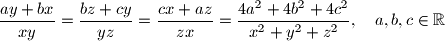
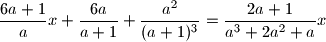 u ovisnosti o realnom parametru
u ovisnosti o realnom parametru  .
.