Odredi najveći prirodni broj

takav da postoji niz od

realnih brojeva sa sljedećim svojstvima:
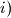
zbroj svaka tri uzastopna člana niza je pozitivan,
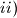
zbroj svakih pet uzastopnih članova niza je negativan.
%V0
Odredi najveći prirodni broj $n$ takav da postoji niz od $n$ realnih brojeva sa sljedećim svojstvima:
$i)$ zbroj svaka tri uzastopna člana niza je pozitivan,
$ii)$ zbroj svakih pet uzastopnih članova niza je negativan.