Neka je

prirodan broj s parnim brojem

znamenaka, a

broj dobiven bilo kojom promjenom poretka znamenaka broja

, tako da vrijedi
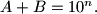

Odredi barem jedan par brojeva

i

koji zadovoljavaju gornje svojstvo za
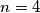
.

Dokaži da je za svaki parni broj

svaki od brojeva

i

s gornjim svojstvom djeljiv s

.
%V0
Neka je $A$ prirodan broj s parnim brojem $n$ znamenaka, a $B$ broj dobiven bilo kojom promjenom poretka znamenaka broja $A$, tako da vrijedi $A+B=10^n.$
$a)$ Odredi barem jedan par brojeva $A$ i $B$ koji zadovoljavaju gornje svojstvo za $n=4$.
$b)$ Dokaži da je za svaki parni broj $n$ svaki od brojeva $A$ i $B$ s gornjim svojstvom djeljiv s $10$.