Školjka

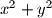Dana je ploča $n \times n$, čiji su retci numerirani brojevima od $1$ do $n$ odozgo prema dolje i stupci brojevima od $1$ do $n$ s lijeva na desno. U svakom polju ploče s koordinatama $(x,y)$ napisan je broj $x^2+y^2$. Na početku nam je dana figura i možemo je postaviti na proizvoljno polje ploče. Nakon toga, u svakom potezu možemo pomaknuti figuru na neko drugo polje ukoliko to polje već nije bilo posjećeno i ako je zadovoljen barem jedan od dva sljedeća uvjeta: \begin{itemize} \item brojevi napisani na ta dva polja daju isti ostatak pri dijeljenju s $n$, \item ta polja se nalaze centralno simetrično u odnosu na sredinu ploče. \end{itemize} Mogu li sva polja ploče biti posjećena ako je a) 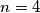$n=4$, b) 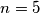$n=5$? \begin{flushright}\emph{(Josip Pupić)}\end{flushright}