Europski matematički kup 2016. seniori 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Dane su kružnice 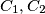 koje se sjeku u točkama
koje se sjeku u točkama 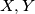 . Neka su točke
. Neka su točke 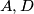 na kružnici
na kružnici  te
te 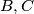 na kružnici
na kružnici  takve da su točke
takve da su točke 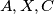 kolinearne te da su točke
kolinearne te da su točke 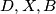 kolinearne. Tangenta na kružnicu
kolinearne. Tangenta na kružnicu  povučenu u točki
povučenu u točki  siječe pravac
siječe pravac  i tangentu na kružnicu
i tangentu na kružnicu  povučenu u
povučenu u  u točkama
u točkama 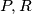 redom. Tangenta na kružnicu
redom. Tangenta na kružnicu  povučenu u točki
povučenu u točki  siječe pravac
siječe pravac  i tangentu na kružnicu
i tangentu na kružnicu  povučenu u
povučenu u  u točkama
u točkama 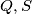 redom. Neka je točka
redom. Neka je točka 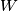 sjecište pravca
sjecište pravca  s tangentom na
s tangentom na  kroz
kroz  , te točka
, te točka  sjecište pravca
sjecište pravca  s tangentom na
s tangentom na  kroz
kroz  . Dokaži da opisane kružnice trokuta
. Dokaži da opisane kružnice trokuta 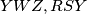 i
i 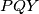 imaju dvije zajedničke točke, ili se dodiruju u jednoj točki.
imaju dvije zajedničke točke, ili se dodiruju u jednoj točki.
(Misiakos Panagiotis)
Izvor: Europski matematički kup 2016.
 Školjka
Školjka 
