Europski matematički kup 2017. seniori 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je  raznostraničan trokut te neka njegova upisana kružnica dodiruje stranice
raznostraničan trokut te neka njegova upisana kružnica dodiruje stranice 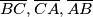 u točkama
u točkama 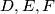 , redom. Neka je
, redom. Neka je  drugo sjecište pravca
drugo sjecište pravca  i te kružnice. Točka
i te kružnice. Točka  odabrana je na pravcu
odabrana je na pravcu 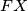 tako da je četverokut
tako da je četverokut 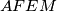 tetivan. Neka se pravci
tetivan. Neka se pravci 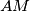 i
i  sijeku u točki
sijeku u točki  te neka je
te neka je  polovište dužine
polovište dužine 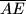 . Točka
. Točka  dana je na pravcu
dana je na pravcu 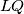 tako da je četverokut
tako da je četverokut 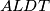 tetivan. Neka je
tetivan. Neka je  točka takva da je četverokut
točka takva da je četverokut 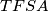 paralelogram te neka je
paralelogram te neka je  drugo sjecište opisane kružnice trokuta
drugo sjecište opisane kružnice trokuta 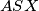 i pravca
i pravca 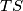 . Dokaži da se opisane kružnice trokuta
. Dokaži da se opisane kružnice trokuta 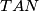 i
i 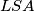 dodiruju.
dodiruju.
(Andrej Ilievski)
Izvor: Europski matematički kup 2017.
 Školjka
Školjka 
