Europski matematički kup 2018. seniori 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je  trokut takav da
trokut takav da 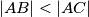 . Neka mu je
. Neka mu je  opisana kružnica sa središtem u
opisana kružnica sa središtem u  . Točka
. Točka  je polovište luka
je polovište luka 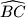 kružnice
kružnice  koji ne sadrži
koji ne sadrži  . Neka je
. Neka je  drugo sjecište okomice iz
drugo sjecište okomice iz  na
na  s
s  , a
, a  drugo sjecište okomice iz
drugo sjecište okomice iz  na
na  s
s  . Neka su
. Neka su  i
i  sjecišta
sjecišta  i
i  sa
sa 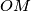 redom. Označimo s
redom. Označimo s 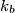 i
i 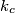 kružnice opisane trokutima
kružnice opisane trokutima 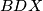 i
i 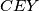 redom. Neka su
redom. Neka su  i
i  druga sjecišta
druga sjecišta 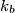 i
i 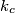 sa
sa  i
i  redom. Označimo sa
redom. Označimo sa 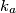 opisanu kružnicu trokuta
opisanu kružnicu trokuta 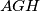 .
.
Dokaži da je  središte opisane kružnice trokuta
središte opisane kružnice trokuta 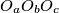 , gdje su
, gdje su 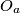 ,
, 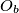 ,
, 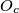 središta
središta 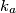 ,
, 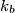 ,
, 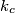 redom.
redom.
(Petar Nizić-Nikolac)
Izvor: Europski matematički kup 2018.
 Školjka
Školjka 
