3. ELMO zadatak 5
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je 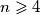 prirodan broj. Promotrimo skup od
prirodan broj. Promotrimo skup od  bakterija, takav da svaka bakterija osim jedne, koju ćemo zvati Kraljica, ima točno jednu majku (također bakteriju iz skupa). Kraljica nema niti jednu majku te je predak svim drugim bakterijama. Nijedna bakterija nije majka sama sebi. Kažemo da je bakterija
bakterija, takav da svaka bakterija osim jedne, koju ćemo zvati Kraljica, ima točno jednu majku (također bakteriju iz skupa). Kraljica nema niti jednu majku te je predak svim drugim bakterijama. Nijedna bakterija nije majka sama sebi. Kažemo da je bakterija  tetka bakterije
tetka bakterije  ako
ako  nije majka od
nije majka od  i majka od
i majka od  je majka majke od
je majka majke od  . Odredi maksimalan broj parova bakterija
. Odredi maksimalan broj parova bakterija 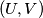 takvih da je
takvih da je  tetka od
tetka od  .
.
(Napomena: Kažemo da je bakterija  predak bakterije
predak bakterije  ako postoji niz bakterija
ako postoji niz bakterija 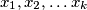 takav da
takav da 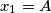 ,
, 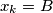 te je
te je 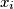 majka
majka 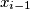 za svaki
za svaki 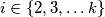 )
)
(Ivan Novak)
Izvor: 3. Ekstremno loša matematička olimpijada
 Školjka
Školjka 
