Slični zadaci
Kvadratna ploča podijeljena je na 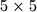 jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
Triomino je lik sastavljen od tri jedinična kvadrata kao na slici:
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Odredi koja sve polja dane kvadratne ploče mogu ostati nepokrivena pri takvom popločavanju.
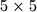 jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.Triomino je lik sastavljen od tri jedinična kvadrata kao na slici:
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Odredi koja sve polja dane kvadratne ploče mogu ostati nepokrivena pri takvom popločavanju.
 Školjka
Školjka 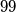 (ne nužno različitih) prirodnih brojeva manjih od
(ne nužno različitih) prirodnih brojeva manjih od  . Ako zbroj nikoja dva, tri ili više od tih brojeva nije djeljiv sa
. Ako zbroj nikoja dva, tri ili više od tih brojeva nije djeljiv sa  prirodnih brojeva postoji njih
prirodnih brojeva postoji njih  , čiji je zbroj djeljiv sa
, čiji je zbroj djeljiv sa  složenih prirodnih brojeva manjih od
složenih prirodnih brojeva manjih od 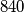 . Dokaži da među njima postoje barem dva broja koja nisu relativno prosta.
. Dokaži da među njima postoje barem dva broja koja nisu relativno prosta.  za koje je
za koje je 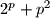 također prost broj.
također prost broj. 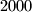 trojki prirodnih brojeva
trojki prirodnih brojeva 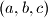 takvih da je
takvih da je 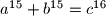 .
.