Slični zadaci
Oko kružnice polumjera  položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.
 položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.  Školjka
Školjka 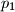 presijeca graf kvadratne funkcije
presijeca graf kvadratne funkcije 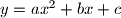 u točkama
u točkama  i
i  . Pravac
. Pravac 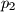 paralelan je pravcu
paralelan je pravcu  i
i  . Dokaži da je suma apscisa točaka
. Dokaži da je suma apscisa točaka  paralelna je s promjerom
paralelna je s promjerom 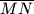 kružnice. Neka je
kružnice. Neka je  tangenta te kružnice u točki
tangenta te kružnice u točki  te neka su točke
te neka su točke 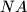 i
i 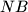 s pravcem
s pravcem 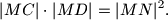
 takav da je maksimalna vrijednost funkcije
takav da je maksimalna vrijednost funkcije 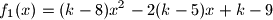 jednaka minimalnoj vrijednosti funkcije
jednaka minimalnoj vrijednosti funkcije 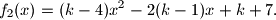
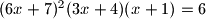 .
. 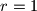 postavljeno je unutar kružnice polumjera
postavljeno je unutar kružnice polumjera  je najmanja vrijednost funkcije
je najmanja vrijednost funkcije 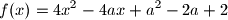 na intervalu
na intervalu ![[0,2]](/media/m/6/8/f/68fca448efcc3c5617dbc68ff5789a46.png) jednaka
jednaka  ?
?