Slični zadaci
U svako polje tablice 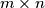 (
(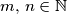 ) upisano je slovo
) upisano je slovo  ili
ili  . Pritom nikoja dva susjedna polja (sa zajedničkom stranicom) ne sadrže isto slovo. U jednom koraku biraju se dva susjedna polja, i oba slova na tim poljima zamijene se novim slovima po sljedećem pravilu:
. Pritom nikoja dva susjedna polja (sa zajedničkom stranicom) ne sadrže isto slovo. U jednom koraku biraju se dva susjedna polja, i oba slova na tim poljima zamijene se novim slovima po sljedećem pravilu:
- umjesto slova upisuje se slovo
upisuje se slovo 
- umjesto slova upisuje se slovo
upisuje se slovo 
- umjesto slova upisuje se slovo
upisuje se slovo  .
.
Za koje i
i  nakon konačno mnogo koraka možemo postići da u svim poljima u kojima je na početku bilo napisano slovo
nakon konačno mnogo koraka možemo postići da u svim poljima u kojima je na početku bilo napisano slovo  sada piše slovo
sada piše slovo  , a u svim poljima u kojima je na početku bilo napisano slovo
, a u svim poljima u kojima je na početku bilo napisano slovo  sada piše slovo
sada piše slovo  ?
?
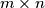 (
(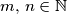 ) upisano je slovo
) upisano je slovo  ili
ili  . Pritom nikoja dva susjedna polja (sa zajedničkom stranicom) ne sadrže isto slovo. U jednom koraku biraju se dva susjedna polja, i oba slova na tim poljima zamijene se novim slovima po sljedećem pravilu:
. Pritom nikoja dva susjedna polja (sa zajedničkom stranicom) ne sadrže isto slovo. U jednom koraku biraju se dva susjedna polja, i oba slova na tim poljima zamijene se novim slovima po sljedećem pravilu:- umjesto slova
 upisuje se slovo
upisuje se slovo 
- umjesto slova
 upisuje se slovo
upisuje se slovo 
- umjesto slova
 upisuje se slovo
upisuje se slovo  .
.Za koje
 i
i  nakon konačno mnogo koraka možemo postići da u svim poljima u kojima je na početku bilo napisano slovo
nakon konačno mnogo koraka možemo postići da u svim poljima u kojima je na početku bilo napisano slovo  sada piše slovo
sada piše slovo  , a u svim poljima u kojima je na početku bilo napisano slovo
, a u svim poljima u kojima je na početku bilo napisano slovo  sada piše slovo
sada piše slovo  ?
? U  posuda (od kojih svaka ima barem
posuda (od kojih svaka ima barem 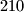 litara) nalazi se redom
litara) nalazi se redom 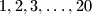 litara vode. Iz posude
litara vode. Iz posude  u posudu
u posudu  dozvoljeno je preliti točno onoliko vode koliko već ima u posudi
dozvoljeno je preliti točno onoliko vode koliko već ima u posudi  (uz pretpostavku da u posudi
(uz pretpostavku da u posudi  ima barem toliko vode koliko u
ima barem toliko vode koliko u  ). Da li je moguće nakon konačno prelijevanja dobiti:
). Da li je moguće nakon konačno prelijevanja dobiti:

 posuda s po
posuda s po  litre vode, a u preostalih
litre vode, a u preostalih  posuda po
posuda po 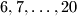 litara;
litara;
 svih
svih 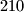 litara vode u jednoj posudi?
litara vode u jednoj posudi?
 posuda (od kojih svaka ima barem
posuda (od kojih svaka ima barem 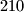 litara) nalazi se redom
litara) nalazi se redom 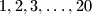 litara vode. Iz posude
litara vode. Iz posude  u posudu
u posudu  dozvoljeno je preliti točno onoliko vode koliko već ima u posudi
dozvoljeno je preliti točno onoliko vode koliko već ima u posudi  (uz pretpostavku da u posudi
(uz pretpostavku da u posudi  ima barem toliko vode koliko u
ima barem toliko vode koliko u  ). Da li je moguće nakon konačno prelijevanja dobiti:
). Da li je moguće nakon konačno prelijevanja dobiti:
 posuda s po
posuda s po  litre vode, a u preostalih
litre vode, a u preostalih  posuda po
posuda po 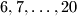 litara;
litara; svih
svih 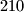 litara vode u jednoj posudi?
litara vode u jednoj posudi? Kvadratna ploča podijeljena je na 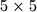 jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
Triomino je lik sastavljen od tri jedinična kvadrata kao na slici:
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Odredi koja sve polja dane kvadratne ploče mogu ostati nepokrivena pri takvom popločavanju.
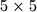 jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.Triomino je lik sastavljen od tri jedinična kvadrata kao na slici:
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Odredi koja sve polja dane kvadratne ploče mogu ostati nepokrivena pri takvom popločavanju.
 Školjka
Školjka 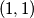 po sljedećim pravilima:
po sljedećim pravilima: iz točke
iz točke 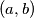 žaba smije skočiti u točku
žaba smije skočiti u točku 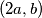 , odnosno
, odnosno 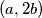 ;
;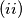 ako je
ako je 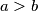 žaba smije skočiti iz
žaba smije skočiti iz 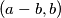 , a ako je
, a ako je 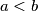 žaba smije skočiti iz
žaba smije skočiti iz 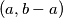 .
.
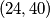 ,
,
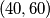 ,
,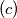
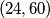 ,
,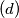
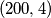 ?
? 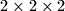 , te se prebroji koliko točaka ima na svakoj strani. Može li se na taj način dobiti šest uzastopnih prirodnih brojeva?
, te se prebroji koliko točaka ima na svakoj strani. Može li se na taj način dobiti šest uzastopnih prirodnih brojeva?  , postoje dva broja čiji je umnožak potpun kvadrat (kvadrat nekog prirodnog broja).
, postoje dva broja čiji je umnožak potpun kvadrat (kvadrat nekog prirodnog broja).