Neka je
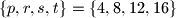
. Promatrajući sve moguće izbore brojeva

,

,

,

, nađite sva rješenja
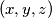
sustava jednadžbi:
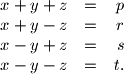
%V0
Neka je $\{p,r,s,t\}=\{4,8,12,16\}$. Promatrajući sve moguće izbore brojeva $p$, $r$, $s$, $t$, nađite sva rješenja $(x,y,z)$ sustava jednadžbi: $$
\begin{array}{lcr}
x+y+z &=& p\\
x+y-z &=& r\\
x-y+z &=& s\\
x-y-z &=& t.
\end{array}
$$