Cilj metode kvocijenata je izraziti jednu nepoznanicu u potpunosti preko druge, i onda komentirati slučajeve kada je izraz cijeli broj.
Lema 1(Zatvorenost na zbrajanje i oduzimanje): Skup cijelih brojeva zatvoren je i s obzirom na zbrajanje i oduzimanje, tj. ukoliko cijelom broju oduzmemo ili pribrojimo drugi cijeli broj, rezultat će i dalje biti cijeli broj. Specijalan slučaj ovoga je: 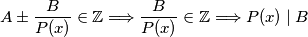
PRIMJER 1:
Riješi diofantsku jednadžbu 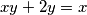 .
.
RJEŠENJE:
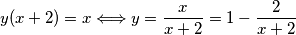 . Sada vidimo da je
. Sada vidimo da je 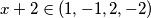 jer mora biti djelitelj od 2 kako bi razlomak bio cjelobrojan, pa je
jer mora biti djelitelj od 2 kako bi razlomak bio cjelobrojan, pa je 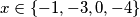 i (daljnjim uvrštavanjem)
i (daljnjim uvrštavanjem) 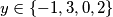 .
.
PRIMJER 2:
Riješi diofantsku jednadžbu: 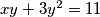
RJEŠENJE:
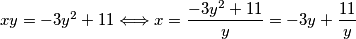 pa je
pa je 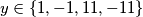 , što daje rješenja redom
, što daje rješenja redom 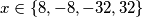 .
.
Zadatci za samostalno rješavanje
1. (Školsko 2019. SŠ1 5.) Odredi sve parove 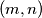 cijelih brojeva za koje vrijedi
cijelih brojeva za koje vrijedi 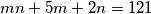
2 (Državno 1998. SŠ1 2.) Nađite sve prirodne brojeve  i
i  koji zadovoljavaju jednadžbu:
koji zadovoljavaju jednadžbu: 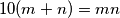
Cilj metode kvocijenata je izraziti jednu nepoznanicu u potpunosti preko druge, i onda komentirati slučajeve kada je izraz cijeli broj.
\textbf{Lema 1}(Zatvorenost na zbrajanje i oduzimanje): Skup cijelih brojeva zatvoren je i s obzirom na zbrajanje i oduzimanje, tj. ukoliko cijelom broju oduzmemo ili pribrojimo drugi cijeli broj, rezultat će i dalje biti cijeli broj. Specijalan slučaj ovoga je: $$A \pm \frac{B}{P(x)} \in \mathbb{Z} \Longrightarrow \frac{B}{P(x)} \in \mathbb{Z} \Longrightarrow P(x) \mid B$$
PRIMJER 1:
Riješi diofantsku jednadžbu $xy + 2y = x$.
RJEŠENJE:
$y(x+2) = x \Longleftrightarrow y = \dfrac{x}{x+2} = 1 - \dfrac{2}{x + 2}$. Sada vidimo da je $x + 2 \in (1, -1, 2, -2)$ jer mora biti djelitelj od 2 kako bi razlomak bio cjelobrojan, pa je $x \in \{-1, -3, 0, -4\}$ i (daljnjim uvrštavanjem) $y \in \{-1, 3, 0, 2\}$.
PRIMJER 2:
Riješi diofantsku jednadžbu: $xy + 3y^2 = 11$
RJEŠENJE:
$xy = -3y^2 + 11 \Longleftrightarrow x = \dfrac{-3y^2 + 11}{y}= -3y + \dfrac{11}{y}$ pa je $y \in \{1, -1, 11, -11\}$, što daje rješenja redom $x \in \{8, -8, -32, 32\}$.
\textbf{Zadatci za samostalno rješavanje}
1. (Školsko 2019. SŠ1 5.) Odredi sve parove $(m, n)$ cijelih brojeva za koje vrijedi $$mn + 5m + 2n = 121$$
2 (Državno 1998. SŠ1 2.) Nađite sve prirodne brojeve $m$ i $n$ koji zadovoljavaju jednadžbu: $$10(m + n)=mn$$
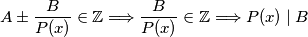
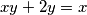 .
.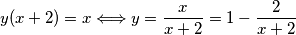 . Sada vidimo da je
. Sada vidimo da je 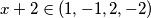 jer mora biti djelitelj od 2 kako bi razlomak bio cjelobrojan, pa je
jer mora biti djelitelj od 2 kako bi razlomak bio cjelobrojan, pa je 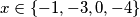 i (daljnjim uvrštavanjem)
i (daljnjim uvrštavanjem) 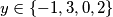 .
.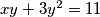
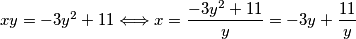 pa je
pa je 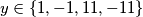 , što daje rješenja redom
, što daje rješenja redom 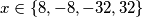 .
.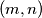 cijelih brojeva za koje vrijedi
cijelih brojeva za koje vrijedi 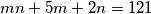
 i
i  koji zadovoljavaju jednadžbu:
koji zadovoljavaju jednadžbu: 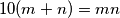
 Školjka
Školjka 
