PRIMJER 1: Odredi zbroj: $\dfrac{1}{1 \cdot 2} + \dfrac{1}{2 \cdot 3} + \dots \dfrac{1}{99 \cdot 100}$.
RJEŠENJE:
Zapišimo neki općeniti član tog niza: $\frac{1}{n \cdot (n+1)}$. Taj razlomak želimo rastaviti na neke razlomke $\frac{A}{n} + \frac{B}{n+1}$. Rješavanjem sustava jednadžbi za konkretne vrijednosti $n$ (npr. $n=1$ i $n=2$) dobivamo $A=1$, $B=-1$. Sada samo trebamo izračunati zbroj: $$\dfrac{1}{1 \cdot 2} + \dfrac{1}{2 \cdot 3} + \dots \dfrac{1}{99 \cdot 100} = \left(\frac{1}{1} - \frac{1}{2}\right) + \left(\frac{1}{2} - \frac{1}{3}\right) + \dots + \left(\frac{1}{99} - \frac{1}{100}\right) = \frac{1}{1} - \frac{1}{100} = \frac{99}{100}$$
PRIMJER 2: Neka je $n \in \mathbb{N}$ takav da je $n>10$. Izračunaj sljedeći umnožak:
$$\frac{2^2-1}{2^2+3\cdot 2+2} \cdot \frac{3^2-1}{3^2+3\cdot 3+2} \cdot \ldots \cdot \frac{n^2-1}{n^2+3n+2} = \prod_{k=2}^n \frac{k^2-1}{k^2+3k+2}$$
RJEŠENJE:
Primijetimo da za svaki $k \in \mathbb{N}$ vrijedi
$$\frac{k^2-1}{k^2+3k+2} = \frac{(k-1)(k+1)}{(k+1)(k+2)} = \frac{k-1}{k+2}$$
Sada je naš umnožak jednak
$$\frac{2-1}{2+2}\cdot \frac{3-1}{3+2} \cdot \frac{4-1}{4+2}\cdot \ldots \cdot \frac{n-1}{n+2} = \frac{1}{4}\cdot \frac{2}{5}\cdot \frac{3}{6}\cdot \ldots \cdot \frac{n-1}{n+2}$$
Primijetimo da će se pokratiti svi brojnici i nazivnici koji su veći od $3$ i manji od $n$, tako da ostaje
$$\frac{1\cdot 2\cdot 3}{n(n+1)(n+2)} = \frac{6}{n(n+1)(n+2)}$$
\textbf{OPREZ:} Uvjet $n>10$ nam je trebao da ne bismo imali preklapanja brojeva koji se nisu pokratili. \\ Na primjer, za $n=3$ ne postoje brojnici niti nazivnici koji su veći od $3$ i manji od $n$, pa \\ treba zasebno argumentirati takav slučaj.
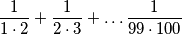 .
.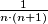 . Taj razlomak želimo rastaviti na neke razlomke
. Taj razlomak želimo rastaviti na neke razlomke 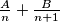 . Rješavanjem sustava jednadžbi za konkretne vrijednosti
. Rješavanjem sustava jednadžbi za konkretne vrijednosti  (npr.
(npr.  i
i  ) dobivamo
) dobivamo 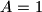 ,
, 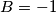 . Sada samo trebamo izračunati zbroj:
. Sada samo trebamo izračunati zbroj: 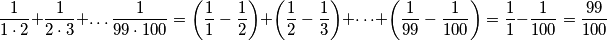
 takav da je
takav da je 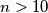 . Izračunaj sljedeći umnožak:
. Izračunaj sljedeći umnožak: 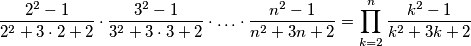
 vrijedi
vrijedi 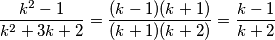 Sada je naš umnožak jednak
Sada je naš umnožak jednak 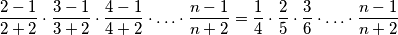 Primijetimo da će se pokratiti svi brojnici i nazivnici koji su veći od
Primijetimo da će se pokratiti svi brojnici i nazivnici koji su veći od  i manji od
i manji od  , tako da ostaje
, tako da ostaje 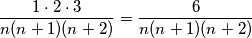
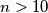 nam je trebao da ne bismo imali preklapanja brojeva koji se nisu pokratili.
nam je trebao da ne bismo imali preklapanja brojeva koji se nisu pokratili. 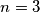 ne postoje brojnici niti nazivnici koji su veći od
ne postoje brojnici niti nazivnici koji su veći od  i manji od
i manji od  , pa
, pa  Školjka
Školjka 
