Slični zadaci
Kružnice  i
i  , polumjera
, polumjera  i
i  redom (
redom (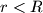 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.
 i
i  , polumjera
, polumjera  i
i  redom (
redom (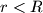 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.  Školjka
Školjka  takve da su tetive
takve da su tetive 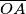 i
i 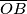 okomite, a
okomite, a 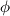 kut između tetive
kut između tetive 
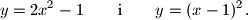
 u Kartezijevoj koordinatnoj ravnini takvih da su tangente povučene iz točke
u Kartezijevoj koordinatnoj ravnini takvih da su tangente povučene iz točke 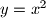 međusobno okomite.
međusobno okomite.  ,
,  ,
,  ,
,  ,
,  i
i  točke u istoj ravnini takve da su trokuti
točke u istoj ravnini takve da su trokuti  ,
, 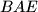 ,
, 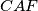 ,
, 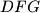 ,
, 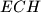 i
i 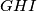 pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka
pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka 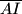 .
.  je polovište tetive parabole
je polovište tetive parabole 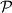 u čijim su krajevima povučene tangente na tu parabolu. Neka je
u čijim su krajevima povučene tangente na tu parabolu. Neka je  sjecište tih tangenata. Dokaži da polovište dužine
sjecište tih tangenata. Dokaži da polovište dužine 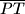 leži na paraboli.
leži na paraboli. 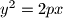 ,
, 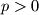 . Na paraboli su dane točke
. Na paraboli su dane točke  paralelna s
paralelna s  -osi. Ako je duljina projekcije dužine
-osi. Ako je duljina projekcije dužine  na
na  -os jednaka
-os jednaka 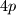 , odredi ordinatu polovišta dužine
, odredi ordinatu polovišta dužine  .
.