Što je veće
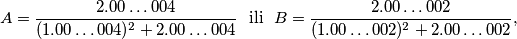
gdje u svakom broju u brojniku i nazivniku ima po
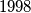
nula?
%V0
Što je veće $$A = \frac{2.00\ldots004}{(1.00\ldots004)^2 + 2.00\ldots004} \,\,\,\, \text{ili} \,\,\,\, B = \frac{2.00\ldots002}{(1.00\ldots002)^2 + 2.00\ldots002}\text{,}$$ gdje u svakom broju u brojniku i nazivniku ima po $1998$ nula?