Junior Balkan MO 2002 - Problem 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 4,0Two circles with centers 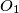 and
and 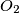 meet at two points
meet at two points  and
and  such that the centers of the circles are on opposite sides of the line
such that the centers of the circles are on opposite sides of the line 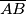 . The lines
. The lines 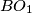 and
and 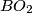 meet their respective circles again at
meet their respective circles again at 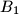 and
and 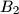 . Let
. Let  be the midpoint of
be the midpoint of 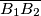 . Let
. Let 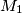 ,
, 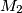 be points on the circles of centers
be points on the circles of centers 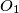 and
and 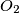 respectively, such that
respectively, such that 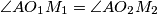 , and
, and 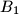 lies on the minor arc
lies on the minor arc 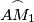 while
while  lies on the minor arc
lies on the minor arc 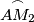 . Show that
. Show that 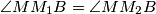 .
.
Izvor: Juniorska balkanska matematička olimpijada 2002.
 Školjka
Školjka 
