Junior Balkan MO 2003 - Problem 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 4,0Let  ,
,  ,
,  be the midpoints of the arcs
be the midpoints of the arcs 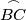 ,
, 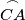 ,
, 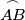 on the circumcircle of a triangle
on the circumcircle of a triangle  not containing the points
not containing the points  ,
,  ,
,  , respectively. Let the line
, respectively. Let the line 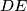 meets
meets  and
and  at
at  and
and  , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 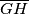 . Let the line
. Let the line 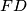 meet
meet  and
and  at
at  and
and 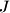 , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 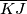 .
.
a) Find the angles of triangle 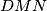 ;
;
b) Prove that if  is the point of intersection of the lines
is the point of intersection of the lines  and
and  , then the circumcenter of triangle
, then the circumcenter of triangle 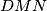 lies on the circumcircle of triangle
lies on the circumcircle of triangle 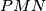 .
.
Izvor: Juniorska balkanska matematička olimpijada 2003.
 Školjka
Školjka 
