Školjka

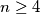Consider a convex polygon having $n$ vertices, $n\geq 4$. We arbitrarily decompose the polygon into triangles having all the vertices among the vertices of the polygon, such that no two of the triangles have interior points in common. We paint in black the triangles that have two sides that are also sides of the polygon, in red if only one side of the triangle is also a side of the polygon and in white those triangles that have no sides that are sides of the polygon. Prove that there are two more black triangles than white ones.