Junior Balkan MO 2005 - Problem 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 4,0Let  be an acute-angled triangle inscribed in a circle
be an acute-angled triangle inscribed in a circle  . It is given that the tangent from
. It is given that the tangent from  to the circle meets the line
to the circle meets the line  at point
at point  . Let
. Let  be the midpoint of the line segment
be the midpoint of the line segment 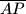 and
and  be the second intersection point of the circle
be the second intersection point of the circle  with the line
with the line 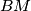 . The line
. The line 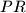 meets again the circle
meets again the circle  at point
at point  different from
different from  .
.
Prove that the lines 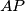 and
and 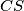 are parallel.
are parallel.
Izvor: Juniorska balkanska matematička olimpijada 2005.
 Školjka
Školjka 
