
Ako su

,
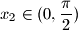
, dokažite:
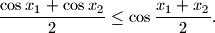

Ako su

,
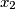
,

,
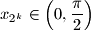
, dokažite:
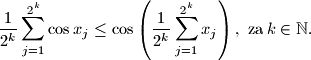
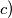
Ako su

,
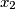
,

,
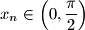
, dokažite:
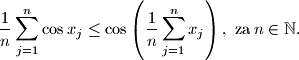
%V0
$a)$ Ako su $x_1$, $x_2\in (0,\displaystyle\frac{\pi }{2})$, dokažite: $$
\frac{\cos x_1+\cos x_2}{2}\leq \cos \frac{x_1+x_2}{2}.
$$ $b)$ Ako su $x_1$, $x_2$, $\dots$, $x_{2^k}\in \left(0,\displaystyle\frac{\pi}{2}\right)$, dokažite: $$
\frac{1}{2^k} \sum _{j=1}^{2^k} \cos x_j \leq \cos \left( \dfrac{1}{2^k} \sum_{j=1}^{2^k} x_j \right), \,\, \text{za} \, k \in \mathbb{N} \text{.}
$$ $c)$ Ako su $x_1$, $x_2$, $\dots$, $x_n\in \left(0,\displaystyle\frac{\pi}{2}\right)$, dokažite: $$
\frac{1}{n} \sum _{j=1}^{n} \cos x_j \leq \cos \left( \dfrac{1}{n} \sum_{j=1}^{n}x_j \right), \,\, \text{za} \, n \in \mathbb{N} \text{.}
$$