Junior Balkan MO 2017 - Problem 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 4,0Consider a regular  -gon
-gon  ,
,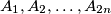 in the plane, where
in the plane, where  is a positive integer. We say that a point
is a positive integer. We say that a point  on one of the sides of
on one of the sides of  can be seen from a point
can be seen from a point  that is external to
that is external to  , if the line segment
, if the line segment 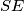 contains no other points that lie on the sides of
contains no other points that lie on the sides of  except
except  . We color the sides of
. We color the sides of  in 3 different colors (ignore the vertices of
in 3 different colors (ignore the vertices of  , we consider them colorless), such that every side is colored in exactly one color, and each color is used at least once. Moreover, from every point in the plane external to
, we consider them colorless), such that every side is colored in exactly one color, and each color is used at least once. Moreover, from every point in the plane external to  , points of most 2 different colors on
, points of most 2 different colors on  can be seen. Find the number of distinct such colorings of
can be seen. Find the number of distinct such colorings of  (two colorings are considered distinct if at least one of sides is colored differently).
(two colorings are considered distinct if at least one of sides is colored differently).
Izvor: Juniorska balkanska matematička olimpijada 2017.
 Školjka
Školjka 
