Unutar kruga polumjera

nalazi se

različitih točaka

,
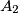
,

,
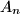
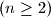
. Za
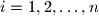
neka
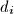
označava udaljenost od
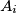
do najbliže od preostalih točaka. Dokaži da vrijedi
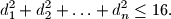
%V0
Unutar kruga polumjera $1$ nalazi se $n$ različitih točaka $A_1$, $A_2$, $\dots$, $A_n$ $(n\geq 2)$. Za $i=1,2,\ldots ,n$ neka $d_i$ označava udaljenost od $A_i$ do najbliže od preostalih točaka. Dokaži da vrijedi $$
d_1^2+d_2^2+\ldots +d_n^2\leq 16.
$$