Zadana je hiperbola sa središtem  . Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama
. Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama  i
i  tako da je
tako da je 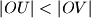 . Neka je točka
. Neka je točka  presjek okomice na realnu os hiperbole u točki
presjek okomice na realnu os hiperbole u točki  i polukružnice s promjerom
i polukružnice s promjerom 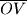 . Dokaži da je
. Dokaži da je 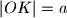 , pri čemu je
, pri čemu je  duljina realne poluosi dane hiperbole.
duljina realne poluosi dane hiperbole.
 . Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama
. Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama  i
i  tako da je
tako da je 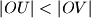 . Neka je točka
. Neka je točka  presjek okomice na realnu os hiperbole u točki
presjek okomice na realnu os hiperbole u točki  i polukružnice s promjerom
i polukružnice s promjerom 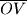 . Dokaži da je
. Dokaži da je 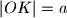 , pri čemu je
, pri čemu je  duljina realne poluosi dane hiperbole.
duljina realne poluosi dane hiperbole. Slični zadaci
Kružnice  i
i  , polumjera
, polumjera  i
i  redom (
redom (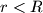 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.
 i
i  , polumjera
, polumjera  i
i  redom (
redom (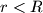 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.  Školjka
Školjka  na jednakostraničnoj hiperboli iz
na jednakostraničnoj hiperboli iz 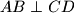 slijedi
slijedi 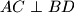 i
i 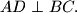
 se giba po koordinatnoj ravnini tako da je produkt njezinih udaljenosti od pravaca
se giba po koordinatnoj ravnini tako da je produkt njezinih udaljenosti od pravaca 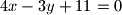 i
i 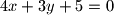 jednak
jednak 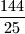 . Nađite jednadžbu geometrijskog mjesta točaka
. Nađite jednadžbu geometrijskog mjesta točaka  ,
,  ,
,  ,
,  i
i  točke u istoj ravnini takve da su trokuti
točke u istoj ravnini takve da su trokuti  ,
, 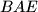 ,
, 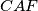 ,
, 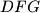 ,
, 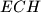 i
i 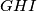 pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka
pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka 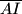 .
. 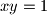 u četiri točke
u četiri točke 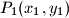 ,break
,break 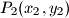 ,
, 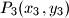 ,
, 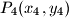 . Dokaži da vrijedi:
. Dokaži da vrijedi:
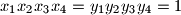 ,
,
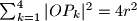 (
(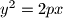 ,
, 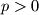 . Na paraboli su dane točke
. Na paraboli su dane točke  paralelna s
paralelna s  -osi. Ako je duljina projekcije dužine
-osi. Ako je duljina projekcije dužine  na
na  -os jednaka
-os jednaka 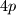 , odredi ordinatu polovišta dužine
, odredi ordinatu polovišta dužine  .
.