Neka je
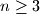
prirodni broj. U kružnicu je upisan

-terokut
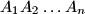
. Dokaži da postoje tri vrha
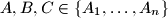
za koje vrijedi
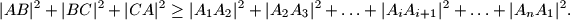
%V0
Neka je $n\ge 3$ prirodni broj. U kružnicu je upisan $n$-terokut $A_1A_2\ldots A_n$. Dokaži da postoje tri vrha $A,B,C\in\{A_1,\ldots,A_n\}$ za koje vrijedi $$
|AB|^2+|BC|^2+|CA|^2\ge |A_1A_2|^2+|A_2A_3|^2+\ldots+|A_iA_{i+1}|^2+\ldots+|A_nA_1|^2.
$$