Kružnice  i
i  , polumjera
, polumjera  i
i  redom (
redom (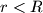 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.
 i
i  , polumjera
, polumjera  i
i  redom (
redom (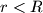 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.  Školjka
Školjka