Slični zadaci
Neka je skup prirodnih brojeva podijeljen u intervale na sljedeći način:
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.
a) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 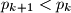 .
.
b) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 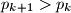 .
.
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je
 udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.a) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 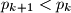 .
.b) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 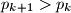 .
.  Školjka
Školjka 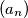 takav da je
takav da je 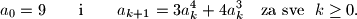 Dokaži da dekadski zapis broja
Dokaži da dekadski zapis broja 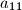 završava s barem
završava s barem 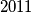 devetki.
devetki. 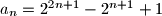 i
i 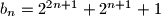 ;
;  . Dokaži da je, za svaki
. Dokaži da je, za svaki  i
i 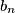 djeljiv s
djeljiv s  .
. 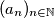 zadan je rekurzivno:
zadan je rekurzivno: 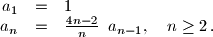 Dokažite da su svi članovi tog niza prirodni brojevi.
Dokažite da su svi članovi tog niza prirodni brojevi. 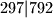 (tj.
(tj. 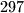 dijeli
dijeli 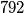 )?
)? 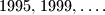 Dokažite da taj niz sadrži beskonačno mnogo prostih brojeva.
Dokažite da taj niz sadrži beskonačno mnogo prostih brojeva. 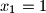 ,
, 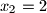 ,
, 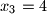 ,
, 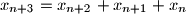 , za svako
, za svako