Slični zadaci
Zadane su kružnica i tetiva koja dijeli njezinu nutrinu na dva kružna odsječka. U njih su upisane kružnice  i
i  koje iznutra diraju kružniuc
koje iznutra diraju kružniuc  , i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica
, i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica  i
i  konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom.
konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom.
 i
i  koje iznutra diraju kružniuc
koje iznutra diraju kružniuc  , i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica
, i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica  i
i  konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom.
konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom.  Školjka
Školjka  vrijedi
vrijedi 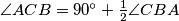 , a
, a  je polovište dužine
je polovište dužine  . Kružnica sa središtem u točki
. Kružnica sa središtem u točki  siječe pravac
siječe pravac  u točkama
u točkama  .
.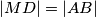 .
. 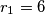 i
i 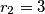 dodiruju se izvana. obje kruznice dodiruju iznutra kruznicu
dodiruju se izvana. obje kruznice dodiruju iznutra kruznicu 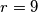 . zajednica vanjska tangenta kruznica
. zajednica vanjska tangenta kruznica  i
i  . izracunajte duljinu tetive
. izracunajte duljinu tetive 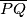 .
.  ,
,  i
i  , a
, a  je duljina polumjera opisane mu kružnice. Odredite kutove trokuta ako vrijedi
je duljina polumjera opisane mu kružnice. Odredite kutove trokuta ako vrijedi 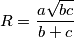 .
.  i
i  sa zajedničkim početkom
sa zajedničkim početkom  dane su točke
dane su točke  (na
(na  i
i  paralelan s težišnicom trokuta
paralelan s težišnicom trokuta 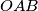 , dokažite da je pravac
, dokažite da je pravac  paralelan s težišnicom trokuta
paralelan s težišnicom trokuta 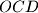 .
.