Dana je dvadeset i jedna točka kao na slici.
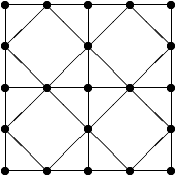
Na početku je svakoj točki pridružen broj nula. U svakom potezu odabire se pravac koji sadrži neku od nacrtanih dužina i u svim točkama kroz koje taj pravac prolazi, pridruženi brojevi se povećavaju za .
.
Kažemo da je prirodni broj dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj
dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj  .
.
a) Dokaži da je broj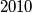 dohvatljiv.
dohvatljiv.
b) Dokaži da broj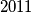 nije dohvatljiv.
nije dohvatljiv.

Na početku je svakoj točki pridružen broj nula. U svakom potezu odabire se pravac koji sadrži neku od nacrtanih dužina i u svim točkama kroz koje taj pravac prolazi, pridruženi brojevi se povećavaju za
 .
.Kažemo da je prirodni broj
 dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj
dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj  .
.a) Dokaži da je broj
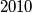 dohvatljiv.
dohvatljiv.b) Dokaži da broj
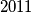 nije dohvatljiv.
nije dohvatljiv. Slični zadaci
Dva igrača,  i
i  igraju sljedeću igru:
igraju sljedeću igru:  i
i  zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od
zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od  . Igrač
. Igrač  igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač
igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač  pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s
pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s  ,
,  ili
ili  , a u suprotnom pobjeđuje igrač
, a u suprotnom pobjeđuje igrač  . Dokaži da igrač
. Dokaži da igrač  ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača
ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača  .
.
 i
i  igraju sljedeću igru:
igraju sljedeću igru:  i
i  zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od
zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od  . Igrač
. Igrač  igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač
igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač  pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s
pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s  ,
,  ili
ili  , a u suprotnom pobjeđuje igrač
, a u suprotnom pobjeđuje igrač  . Dokaži da igrač
. Dokaži da igrač  ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača
ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača  .
.  Školjka
Školjka 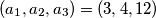 . Provodimo sljedeći postupak: biramo dva broja,
. Provodimo sljedeći postupak: biramo dva broja,  i
i 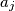 ,
, 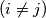 , te ih zamijenimo sa
, te ih zamijenimo sa 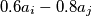 i
i 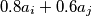 . Može li se višekratnom primjenom gore opisanog postupka dobiti trojka
. Može li se višekratnom primjenom gore opisanog postupka dobiti trojka 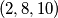 ?
?  ,
,  ,
,  lipa i od
lipa i od  lipa može isplatiti pomoću
lipa može isplatiti pomoću  kovanica, onda se iznos od
kovanica, onda se iznos od 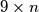 može prekriti pločicama oblika
može prekriti pločicama oblika  tako da se one međusobno ne preklapaju?
tako da se one međusobno ne preklapaju?  odjeljaka u koje su upisani brojevi
odjeljaka u koje su upisani brojevi  ,
, 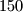 , ...,
, ..., 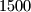 (u nekom redoslijedu). Dokažite da postoje tri uzastopna odjeljka u kojima je zbroj upisanih brojeva veći ili jednak
(u nekom redoslijedu). Dokažite da postoje tri uzastopna odjeljka u kojima je zbroj upisanih brojeva veći ili jednak 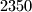 .
. 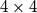 može obojiti u dvije boje tako da za svaki izbor dvaju redaka i dvaju stupaca vrijedi da četiri polja u presjecima tih redaka i stupaca nisu sva obojana istom bojom.
može obojiti u dvije boje tako da za svaki izbor dvaju redaka i dvaju stupaca vrijedi da četiri polja u presjecima tih redaka i stupaca nisu sva obojana istom bojom.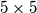 .
.