Neka su

,

i

tri različita realna broja od kojih niti jedan nije jednak nula. Promatramo kvadratne jednadžbe:
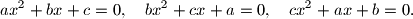
Ako je
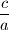
rješenje prve jednadžbe, dokaži da sve tri jednadžbe imaju zajedničko rješenje.
Odredi umnožak drugih triju rješenja tih jednadžbi (ne-zajedničkih).
%V0
Neka su $a$, $b$ i $c$ tri različita realna broja od kojih niti jedan nije jednak nula. Promatramo kvadratne jednadžbe: $$
a x^2 + b x + c= 0, \quad b x^2 + c x + a= 0, \quad c x^2 + a x +
b= 0.
$$
Ako je $\dfrac{c}{a}$ rješenje prve jednadžbe, dokaži da sve tri jednadžbe imaju zajedničko rješenje.
Odredi umnožak drugih triju rješenja tih jednadžbi (ne-zajedničkih).