Slični zadaci
Dane su dvije kružnice  i
i  koje nemaju zajedničkih točaka. Zajedničke vanjske tangente,
koje nemaju zajedničkih točaka. Zajedničke vanjske tangente, 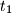 i
i 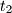 , diraju kružnicu
, diraju kružnicu  u točkama
u točkama  i
i 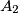 , a kružnicu
, a kružnicu  u točkama
u točkama  i
i 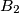 . Zajedničke unutarnje tangente,
. Zajedničke unutarnje tangente, 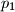 i
i 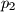 , diraju kružnicu
, diraju kružnicu  u točkama
u točkama  i
i  , a kružnicu
, a kružnicu  u točkama
u točkama 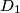 i
i 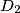 . Dokažite da je udaljenost pravaca
. Dokažite da je udaljenost pravaca 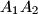 i
i 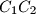 jednaka udaljenosti pravaca
jednaka udaljenosti pravaca 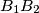 i
i 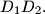
 i
i  koje nemaju zajedničkih točaka. Zajedničke vanjske tangente,
koje nemaju zajedničkih točaka. Zajedničke vanjske tangente, 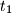 i
i 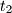 , diraju kružnicu
, diraju kružnicu  u točkama
u točkama  i
i 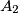 , a kružnicu
, a kružnicu  u točkama
u točkama  i
i 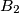 . Zajedničke unutarnje tangente,
. Zajedničke unutarnje tangente, 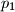 i
i 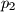 , diraju kružnicu
, diraju kružnicu  u točkama
u točkama  i
i  , a kružnicu
, a kružnicu  u točkama
u točkama 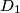 i
i 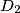 . Dokažite da je udaljenost pravaca
. Dokažite da je udaljenost pravaca 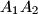 i
i 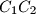 jednaka udaljenosti pravaca
jednaka udaljenosti pravaca 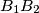 i
i 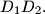
 Školjka
Školjka  kvadrat stranice
kvadrat stranice  . Kružnica
. Kružnica  ima polumjer
ima polumjer  . Odredi polumjer kružnice
. Odredi polumjer kružnice 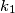 koja dira kružnicu
koja dira kružnicu  i
i 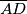 .
. 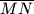 kružnice. Neka je
kružnice. Neka je  tangenta te kružnice u točki
tangenta te kružnice u točki  te neka su točke
te neka su točke  redom sjecišta pravaca
redom sjecišta pravaca 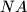 i
i 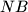 s pravcem
s pravcem 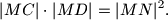
 dane su točke
dane su točke 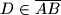 i
i 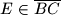 takve da je
takve da je 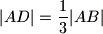 i
i 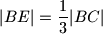 . Pravci
. Pravci  i
i  sijeku se u točki
sijeku se u točki  . Koliki je kut
. Koliki je kut 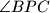 ?
?  i
i  . Kroz točku
. Kroz točku  zadanog pravokutnika. Odredi duljinu one tetive kružnice koja sadrži dijagonalu
zadanog pravokutnika. Odredi duljinu one tetive kružnice koja sadrži dijagonalu  .
.  . Ako dva pravca koja prolaze kroz točku
. Ako dva pravca koja prolaze kroz točku  , a drugu kružnicu u točkama
, a drugu kružnicu u točkama 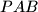 i
i  slični.
slični.