Šahovska ploča
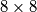
razrezana je na četiri dijela, kao na slici lijevo, od kojih se može
složiti pravokutnik
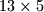
, kao na slici desno. Služeći se kutovima

i

sa slike objasnite dobiveni paradoks
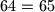
.
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
%V0
Šahovska ploča $8 \times 8$ razrezana je na četiri dijela, kao na slici lijevo, od kojih se može
složiti pravokutnik $13 \times 5$, kao na slici desno. Služeći se kutovima $\alpha$ i $\beta$ sa slike objasnite dobiveni paradoks $64 = 65$.
[img attachment=1 width=500px]