U raznostraničnom šiljastokutnom trokutu

povučene su težišnica
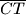
i visina
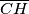
na stranicu

(točke

i

leže na stranici

). Ako su kutovi
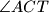
i
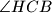
jednaki, dokažite da je trokut pravokutan.
%V0
U raznostraničnom šiljastokutnom trokutu $ABC$ povučene su težišnica $\overline{CT}$ i visina $\overline{CH}$ na stranicu $\overline{AB}$ (točke $T$ i $H$ leže na stranici $\overline{AB}$). Ako su kutovi $\angle ACT$ i $\angle HCB$ jednaki, dokažite da je trokut pravokutan.