Zadan je konveksan četverokut
s kutovima
,
,
i
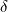
od kojih nijedan nije pravi. Dokažite da vrijedi ovaj identitet
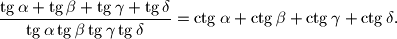
%V0
Zadan je konveksan četverokut $ABCD$ s kutovima $\alpha$, $\beta$, $\gamma$ i $\delta$ od kojih nijedan nije pravi. Dokažite da vrijedi ovaj identitet
$$
\dfrac{\tg \alpha + \tg \beta + \tg \gamma + \tg \delta}{\tg \alpha \tg \beta \tg \gamma \tg \delta} = \ctg \alpha + \ctg \beta + \ctg \gamma + \ctg \delta \text{.}
$$
Školjka