Dokažite da sjecište visina šiljastokutnog trokuta

s danim kutovima

,

i

, dijeli njegovu visinu iz vrha

u omjeru
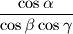
.
%V0
Dokažite da sjecište visina šiljastokutnog trokuta $ABC$ s danim kutovima $\alpha $, $\beta $ i $\gamma $, dijeli njegovu visinu iz vrha $A$ u omjeru $ \dfrac{\cos \alpha}{\cos \beta \cos \gamma }$.