Koliko najmanje elemenata treba izbaciti iz skupa
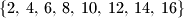
tako da umnožak preostalih elemenata bude kvadrat prirodnog broja?
%V0
Koliko najmanje elemenata treba izbaciti iz skupa $$\left\{2,\,4,\,6,\,8,\,10,\,12,\,14,\,16\right\}$$ tako da umnožak preostalih elemenata bude kvadrat prirodnog broja?