Prvo kolo
na "cetvrtini" beskonacne kvadratne mreze ( tamo gdje je 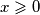 i
i 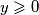 ), igra se sljedeca igra: u kvadraticima s koordinatama
), igra se sljedeca igra: u kvadraticima s koordinatama 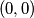 ,
, 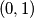 ,
, 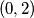 ,
, 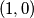 ,
, 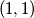 ,
, 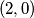 postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja
postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja 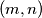 , gdje su
, gdje su 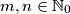 takvi da na poljima
takvi da na poljima 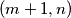 i
i 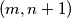 ne stoji zeton, te staviti po jedan zeton na polje
ne stoji zeton, te staviti po jedan zeton na polje 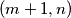 i na polje
i na polje 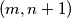 . je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
. je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
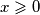 i
i 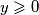 ), igra se sljedeca igra: u kvadraticima s koordinatama
), igra se sljedeca igra: u kvadraticima s koordinatama 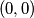 ,
, 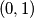 ,
, 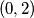 ,
, 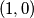 ,
, 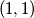 ,
, 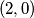 postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja
postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja 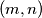 , gdje su
, gdje su 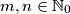 takvi da na poljima
takvi da na poljima 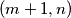 i
i 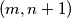 ne stoji zeton, te staviti po jedan zeton na polje
ne stoji zeton, te staviti po jedan zeton na polje 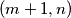 i na polje
i na polje 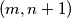 . je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
. je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton? Kiki zamisli dvoznamenkasti broj, a Veki ga pokušava pogoditi. Ako Veki pogodi točan broj ili broj kojemu je jedna znamenka točna a druga se od točne razlikuje za 1 Kiki mu kaže "Toplo!", inače kaže "Hladno!". (npr. ako Kiki zamisli 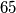 , za pogađane brojeve
, za pogađane brojeve 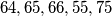 reći će "Toplo!", a za ostale "Hladno!")
reći će "Toplo!", a za ostale "Hladno!")
 Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od
Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od 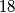 pokušaja.
pokušaja.
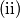 Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od
Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od 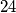 pokušaja.
pokušaja.
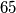 , za pogađane brojeve
, za pogađane brojeve 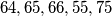 reći će "Toplo!", a za ostale "Hladno!")
reći će "Toplo!", a za ostale "Hladno!")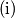 Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od
Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od 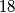 pokušaja.
pokušaja.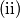 Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od
Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od 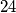 pokušaja.
pokušaja. Dan je raznostraničan šiljastokutan trokut  . Neka je
. Neka je  sjecište vanjske simetrale kuta
sjecište vanjske simetrale kuta 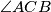 i pravca
i pravca  . Neka je
. Neka je  točka na kružnici opisanoj trokutu
točka na kružnici opisanoj trokutu  takva da je
takva da je 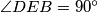 . Neka je
. Neka je  na istoj toj kružnici, tako da leži na manjem kružnom luku
na istoj toj kružnici, tako da leži na manjem kružnom luku  . Točka
. Točka  je sjecište pravaca
je sjecište pravaca 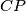 i
i 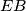 . Dokažite da je pravac
. Dokažite da je pravac 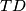 okomit na pravac
okomit na pravac  ako i samo ako vrijedi:
ako i samo ako vrijedi: 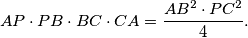
 . Neka je
. Neka je  sjecište vanjske simetrale kuta
sjecište vanjske simetrale kuta 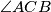 i pravca
i pravca  . Neka je
. Neka je  točka na kružnici opisanoj trokutu
točka na kružnici opisanoj trokutu  takva da je
takva da je 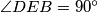 . Neka je
. Neka je  na istoj toj kružnici, tako da leži na manjem kružnom luku
na istoj toj kružnici, tako da leži na manjem kružnom luku  . Točka
. Točka  je sjecište pravaca
je sjecište pravaca 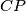 i
i 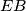 . Dokažite da je pravac
. Dokažite da je pravac 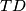 okomit na pravac
okomit na pravac  ako i samo ako vrijedi:
ako i samo ako vrijedi: 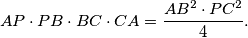
 Školjka
Školjka 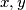 vrijedi nejednakost:
vrijedi nejednakost: 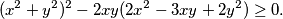 Kada vrijedi jednakost?
Kada vrijedi jednakost?  jediničnih kvadratića tako da ukupan opseg zacrnjenog područja bude minimalan. Odredite koliko iznosi minimalan opseg te jedan način zacrnjivanja za koji se on postiže.
jediničnih kvadratića tako da ukupan opseg zacrnjenog područja bude minimalan. Odredite koliko iznosi minimalan opseg te jedan način zacrnjivanja za koji se on postiže.  . Neka je
. Neka je  u točki
u točki  . Ako je
. Ako je  sjecište pravaca
sjecište pravaca 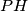 i
i 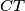 , dokažite da trokuti
, dokažite da trokuti 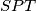 i
i 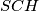 imaju iste površine.
imaju iste površine.  takav da za njegova četiri najmanja djelitelja
takav da za njegova četiri najmanja djelitelja 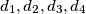 vrijedi:
vrijedi: 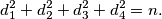
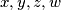 takve da vrijedi:
takve da vrijedi: 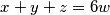
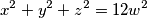
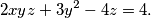
 , a
, a 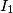 središte upisane kružnice trokuta
središte upisane kružnice trokuta  , a
, a 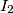 središte upisane kružnice trokuta
središte upisane kružnice trokuta 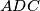 . Dokažite da je
. Dokažite da je 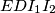 tetivan.
tetivan. 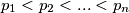 takve da je
takve da je 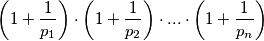 prirodan broj.
prirodan broj.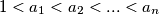 takvi da je
takvi da je 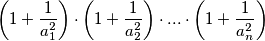 prirodan broj.
prirodan broj.