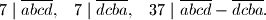Trece kolo
Roko se šeće po ploči 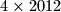 (
( retka,
retka, 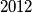 stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
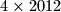 (
( retka,
retka, 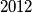 stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu? Pravilni šestrerokuti duljine stranice  poslagani su tako da formiraju igraću ploču u obliku pravilnog šesterokuta stranice
poslagani su tako da formiraju igraću ploču u obliku pravilnog šesterokuta stranice 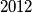 . Vlatko i Vlatka igraju igru na toj ploči. U prvom potezu Vlatko bira mjesto na koje će staviti figuru, a nakon toga, Vlatka pa Vlatko naizmjence pomiču figuru na neko susjedno polje. Tko pomakne figuru na polje na kojem je već bila, gubi. Tko ima pobjedničku strategiju?
. Vlatko i Vlatka igraju igru na toj ploči. U prvom potezu Vlatko bira mjesto na koje će staviti figuru, a nakon toga, Vlatka pa Vlatko naizmjence pomiču figuru na neko susjedno polje. Tko pomakne figuru na polje na kojem je već bila, gubi. Tko ima pobjedničku strategiju?
 poslagani su tako da formiraju igraću ploču u obliku pravilnog šesterokuta stranice
poslagani su tako da formiraju igraću ploču u obliku pravilnog šesterokuta stranice 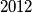 . Vlatko i Vlatka igraju igru na toj ploči. U prvom potezu Vlatko bira mjesto na koje će staviti figuru, a nakon toga, Vlatka pa Vlatko naizmjence pomiču figuru na neko susjedno polje. Tko pomakne figuru na polje na kojem je već bila, gubi. Tko ima pobjedničku strategiju?
. Vlatko i Vlatka igraju igru na toj ploči. U prvom potezu Vlatko bira mjesto na koje će staviti figuru, a nakon toga, Vlatka pa Vlatko naizmjence pomiču figuru na neko susjedno polje. Tko pomakne figuru na polje na kojem je već bila, gubi. Tko ima pobjedničku strategiju?  Školjka
Školjka 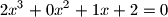 rješenja u skupu realnih brojeva?
rješenja u skupu realnih brojeva?  sijeku se u
sijeku se u  . Kružnica opisana trokutu
. Kružnica opisana trokutu 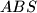 siječe pravac
siječe pravac  u točki
u točki  , a kružnica opisana trokutu
, a kružnica opisana trokutu 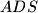 siječe pravac
siječe pravac  u točki
u točki  . Dokažite da su
. Dokažite da su  ima
ima  znamenaka, a dekadski zapis broja
znamenaka, a dekadski zapis broja 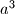 ima
ima  znamenaka. Je li moguće da je
znamenaka. Je li moguće da je 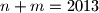 ?
? 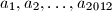 iz intervala
iz intervala ![\left[0,1\right]](/media/m/e/7/f/e7f4d22d3ff05cc9bd2c7aa876c2715c.png) . Dokaži nejednakost:
. Dokaži nejednakost: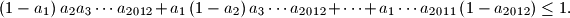
 i točka
i točka  u njegovoj unutrašnjosti. Pravci
u njegovoj unutrašnjosti. Pravci 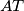 ,
, 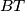 ,
, 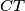 sijeku dužine
sijeku dužine  ,
,  ,
,  u
u  ,
,  ,
,  , respektivno. Neka je
, respektivno. Neka je 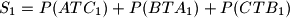 ,
, 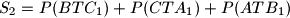 . Dokaži da postoji beskonačno mnogo izbora točke
. Dokaži da postoji beskonačno mnogo izbora točke 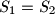 .
.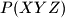 označava provršinu trokuta
označava provršinu trokuta 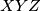 .
. 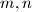 takve da vrijedi:
takve da vrijedi: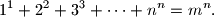
 te neka su
te neka su 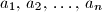 i
i 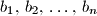 dva niza različitih realnih brojeva. U tablici dimenzija
dva niza različitih realnih brojeva. U tablici dimenzija  broj u
broj u  -tom redu i
-tom redu i  -tom stupcu je jednak
-tom stupcu je jednak 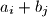 . Produkti brojeva u svakom redu tablice su jednaki. Dokaži da su i produkti brojeva u svakom stupcu tablice također jednaki.
. Produkti brojeva u svakom redu tablice su jednaki. Dokaži da su i produkti brojeva u svakom stupcu tablice također jednaki.  , u kojem nikoje tri točke nisu kolinearne i takav da opišemo li kružnicu bilo kojima trima točkama iz
, u kojem nikoje tri točke nisu kolinearne i takav da opišemo li kružnicu bilo kojima trima točkama iz  promjer opisane kružnice. Neka točke
promjer opisane kružnice. Neka točke  i
i  leže na pravcima
leže na pravcima  i
i  . Dužine
. Dužine 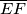 i
i  se sijeku u
se sijeku u  . Dokaži da ako je
. Dokaži da ako je 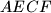 tetivan, da je
tetivan, da je 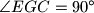 .
. 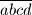 takve da vrijedi
takve da vrijedi