Prvo kolo
Zadane su 2 kružnice,  i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 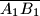 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 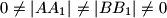 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 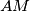 i
i 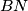 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 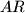 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 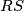 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
.
 i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 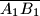 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 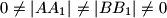 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 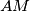 i
i 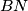 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 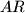 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 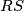 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
. Zadane su 2 kružnice,  i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 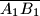 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 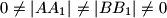 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 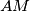 i
i 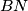 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 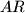 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 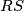 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
.
 i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 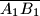 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 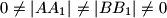 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 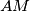 i
i 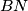 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 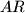 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 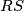 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
.  Školjka
Školjka 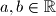 vrijedi
vrijedi 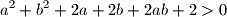
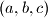 na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s
na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s 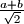 i
i 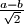 . Možemo li doći do trojke
. Možemo li doći do trojke 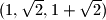 krenuvši od trojke
krenuvši od trojke 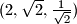 ?
?  simetrale kuta
simetrale kuta  pri vrhu
pri vrhu  siječe nasuprotnu stranicu
siječe nasuprotnu stranicu  izvan trokuta
izvan trokuta 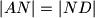 i da je
i da je 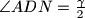 . Dokažite da je
. Dokažite da je  simetrala kuta
simetrala kuta 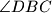 .
. 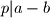 onda
onda 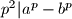
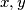 za koje vrijedi
za koje vrijedi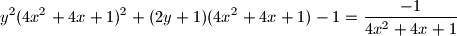
 -članih podskupova skupa
-članih podskupova skupa 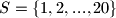 od kojih ni jedan ne sadrži
od kojih ni jedan ne sadrži  uzastopna broja?
uzastopna broja? 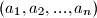 u parovima relativno prosti prirodni brojevi. Dokaži da postoje cijeli brojevi
u parovima relativno prosti prirodni brojevi. Dokaži da postoje cijeli brojevi 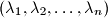 , koji su svi različiti od
, koji su svi različiti od  , takvi da je
, takvi da je 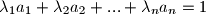 .
. 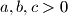 dokaži da vrijedi:
dokaži da vrijedi: 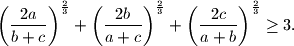
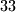 djece. Svakog su pitali koliko ima djece s istim imenom (svatko broji i sebe samog u to), te onda s istim prezimenom (opet svatko broji i sebe samog). Među
djece. Svakog su pitali koliko ima djece s istim imenom (svatko broji i sebe samog u to), te onda s istim prezimenom (opet svatko broji i sebe samog). Među 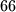 brojeva, svi brojevi od
brojeva, svi brojevi od  do
do  su bili odgovoreni. Dokaži da postoje dvojica s istim imenom i prezimenom.
su bili odgovoreni. Dokaži da postoje dvojica s istim imenom i prezimenom. 