Dan je trokut  i točka
i točka  unutar njega. Pravac paralelan s
unutar njega. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Pravac paralelan s
redom. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i 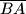 u točkama
u točkama  i
i  redom, dok pravac paralelan s
redom, dok pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Dokaži da vrijedi
redom. Dokaži da vrijedi  gdje
gdje  i
i  označavaju površinu trokuta
označavaju površinu trokuta 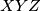 , odnosno površinu četverokuta
, odnosno površinu četverokuta  .
.
 i točka
i točka  unutar njega. Pravac paralelan s
unutar njega. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Pravac paralelan s
redom. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i 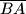 u točkama
u točkama  i
i  redom, dok pravac paralelan s
redom, dok pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Dokaži da vrijedi
redom. Dokaži da vrijedi  gdje
gdje  i
i  označavaju površinu trokuta
označavaju površinu trokuta 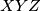 , odnosno površinu četverokuta
, odnosno površinu četverokuta  .
. Dan je lokot sastavljen od  kotačića na kojima su zapisane znamenke
kotačića na kojima su zapisane znamenke 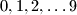 tim redom (nakon
tim redom (nakon  opet dolazi
opet dolazi  ). Točno jedna šifra otključava taj lokot. Jedan potez sastoji se od okretanja jednog od kotačića za jednu znamenku u bilo kojem smjeru, te se lokot odmah otvara ukoliko je novodobivena kombinacija jednaka šifri. Na početku su kotačići okrenuti tako da pokazuju kombinaciju
). Točno jedna šifra otključava taj lokot. Jedan potez sastoji se od okretanja jednog od kotačića za jednu znamenku u bilo kojem smjeru, te se lokot odmah otvara ukoliko je novodobivena kombinacija jednaka šifri. Na početku su kotačići okrenuti tako da pokazuju kombinaciju 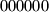 , te je provjereno da ta kombinacija ne otvara lokot.
, te je provjereno da ta kombinacija ne otvara lokot.
a) Koji je najmanji broj poteza koji nam je potreban da sigurno otkrijemo šifru?
b) Koji je najmanji broj poteza koji nam je potreban da sigurno otkrijemo šifru, ako nam je još na početku rečeno da nijedna od kombinacija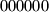 ,
, 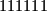 ,
, 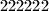 ,
,  ,
, 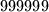 nije šifra za taj lokot?
nije šifra za taj lokot?
 kotačića na kojima su zapisane znamenke
kotačića na kojima su zapisane znamenke 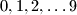 tim redom (nakon
tim redom (nakon  opet dolazi
opet dolazi  ). Točno jedna šifra otključava taj lokot. Jedan potez sastoji se od okretanja jednog od kotačića za jednu znamenku u bilo kojem smjeru, te se lokot odmah otvara ukoliko je novodobivena kombinacija jednaka šifri. Na početku su kotačići okrenuti tako da pokazuju kombinaciju
). Točno jedna šifra otključava taj lokot. Jedan potez sastoji se od okretanja jednog od kotačića za jednu znamenku u bilo kojem smjeru, te se lokot odmah otvara ukoliko je novodobivena kombinacija jednaka šifri. Na početku su kotačići okrenuti tako da pokazuju kombinaciju 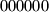 , te je provjereno da ta kombinacija ne otvara lokot.
, te je provjereno da ta kombinacija ne otvara lokot.a) Koji je najmanji broj poteza koji nam je potreban da sigurno otkrijemo šifru?
b) Koji je najmanji broj poteza koji nam je potreban da sigurno otkrijemo šifru, ako nam je još na početku rečeno da nijedna od kombinacija
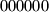 ,
, 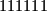 ,
, 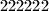 ,
,  ,
, 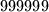 nije šifra za taj lokot?
nije šifra za taj lokot? Niz od  znamenaka jedan ili nula zovemo kodom. Podniz koda je palindrom ako se jednako čita s lijeva na desno i s desna na lijevo. Palindrom zovemo lijepim ako se njegove znamenke u kodu pojavljuju za redom. (Kod
znamenaka jedan ili nula zovemo kodom. Podniz koda je palindrom ako se jednako čita s lijeva na desno i s desna na lijevo. Palindrom zovemo lijepim ako se njegove znamenke u kodu pojavljuju za redom. (Kod 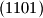 sadrži 10 palindroma, od kojih je 6 lijepih.)
sadrži 10 palindroma, od kojih je 6 lijepih.)
a) Koji je najmanji mogući broj palindroma u kodu?
b) Koji je najmanji mogući broj lijepih palindroma u kodu?
 znamenaka jedan ili nula zovemo kodom. Podniz koda je palindrom ako se jednako čita s lijeva na desno i s desna na lijevo. Palindrom zovemo lijepim ako se njegove znamenke u kodu pojavljuju za redom. (Kod
znamenaka jedan ili nula zovemo kodom. Podniz koda je palindrom ako se jednako čita s lijeva na desno i s desna na lijevo. Palindrom zovemo lijepim ako se njegove znamenke u kodu pojavljuju za redom. (Kod 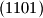 sadrži 10 palindroma, od kojih je 6 lijepih.)
sadrži 10 palindroma, od kojih je 6 lijepih.)a) Koji je najmanji mogući broj palindroma u kodu?
b) Koji je najmanji mogući broj lijepih palindroma u kodu?
 Školjka
Školjka  neka je
neka je 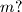 umnožak prvih
umnožak prvih 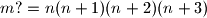 .
.  pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 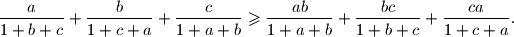
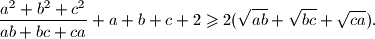
 tablicu zovemo blesavom ako je broj u svakom polju tablice jednak umnošku svih brojeva u susjednim poljima.
tablicu zovemo blesavom ako je broj u svakom polju tablice jednak umnošku svih brojeva u susjednim poljima.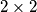 .
.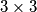 .
.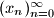 definiranom sa
definiranom sa 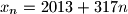 nalazi beskonačno mnogo prirodnih brojeva čiji su decimalni zapisi palindromi.
nalazi beskonačno mnogo prirodnih brojeva čiji su decimalni zapisi palindromi. 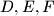 nožišta visina iz
nožišta visina iz 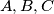 redom. Neka su
redom. Neka su 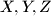 polovišta visina
polovišta visina 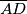 ,
, 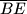 ,
, 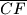 redom. Dokaži da se okomica iz
redom. Dokaži da se okomica iz 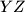 , okomica iz
, okomica iz 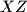 te okomica iz
te okomica iz  sijeku u jednoj točki.
sijeku u jednoj točki.