Dana je ploča  , čiji su retci numerirani brojevima od
, čiji su retci numerirani brojevima od  do
do  odozgo prema dolje i stupci brojevima od
odozgo prema dolje i stupci brojevima od  do
do  s lijeva na desno. U svakom polju ploče s koordinatama
s lijeva na desno. U svakom polju ploče s koordinatama  napisan je broj
napisan je broj 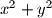 . Na početku nam je dana figura i možemo je postaviti na proizvoljno polje ploče. Nakon toga, u svakom potezu možemo pomaknuti figuru na neko drugo polje ukoliko to polje već nije bilo posjećeno i ako je zadovoljen barem jedan od dva sljedeća uvjeta:
. Na početku nam je dana figura i možemo je postaviti na proizvoljno polje ploče. Nakon toga, u svakom potezu možemo pomaknuti figuru na neko drugo polje ukoliko to polje već nije bilo posjećeno i ako je zadovoljen barem jedan od dva sljedeća uvjeta:  Mogu li sva polja ploče biti posjećena ako je
Mogu li sva polja ploče biti posjećena ako je
a) 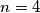 ,
,
b) 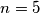 ?
?
(Josip Pupić)
Grupa matematičara nalazi se na konferenciji. Kažemo da je matematičar  -zadovoljan ako je u prostoriji s barem još
-zadovoljan ako je u prostoriji s barem još  ljudi kojima se on divi ili je u prostoriji s barem
ljudi kojima se on divi ili je u prostoriji s barem  ljudi koji se dive njemu. Poznato je da su svi matematičari na konferenciji
ljudi koji se dive njemu. Poznato je da su svi matematičari na konferenciji 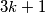 -zadovoljni, ukoliko se svi nalaze u jednoj sobi prostoriji. Dokaži da je sve matematičare moguće podijeliti u dvije prostorije tako da nikoja prostorija nije prazna i tako da svi matematičari barem
-zadovoljni, ukoliko se svi nalaze u jednoj sobi prostoriji. Dokaži da je sve matematičare moguće podijeliti u dvije prostorije tako da nikoja prostorija nije prazna i tako da svi matematičari barem  -zadovoljni. Diviti se nekome nije uzajamna relacija. Nitko se ne divi samome sebi.
-zadovoljni. Diviti se nekome nije uzajamna relacija. Nitko se ne divi samome sebi.
(Matija Bucić)
 Školjka
Školjka 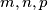 sa svojstvom
sa svojstvom 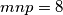 . U ovisnosti o tim konstantama nađi minimum izraza
. U ovisnosti o tim konstantama nađi minimum izraza 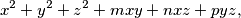 gdje su
gdje su 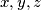 proizvoljni pozitivni realni brojevi takvi da je
proizvoljni pozitivni realni brojevi takvi da je 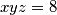 . Kada se postiže jednakost?
. Kada se postiže jednakost?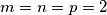 ,
,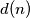 označava broj pozitivnih djelitelja broja
označava broj pozitivnih djelitelja broja  na sljedeći način:
na sljedeći način: 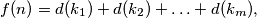 gdje su
gdje su 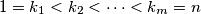 svi djelitelji broja
svi djelitelji broja 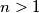 zovemo skoro savršenim ako je
zovemo skoro savršenim ako je 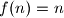 . Nađi sve skoro savršene brojeve.
. Nađi sve skoro savršene brojeve. šiljastokutan trokut. Neka su
šiljastokutan trokut. Neka su 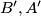 točke na simetralama dužina
točke na simetralama dužina 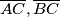 redom takve da je
redom takve da je 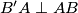 i
i 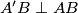 . Neka je
. Neka je  točka na stranici
točka na stranici  i neka je
i neka je  središte opisane kružnice trokutu
središte opisane kružnice trokutu 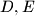 točke na pravcima
točke na pravcima 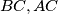 redom takve da je
redom takve da je 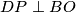 i
i 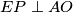 . Neka je
. Neka je 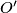 središte opisane kružnice trokuta
središte opisane kružnice trokuta 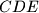 . Dokaži da su točke
. Dokaži da su točke 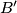 ,
, 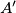 i
i 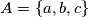 tročlani podskup skupa prirodnih brojeva. Dokaži da postoji podskup
tročlani podskup skupa prirodnih brojeva. Dokaži da postoji podskup 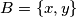 skupa
skupa  takav da je za sve neparne prirodne brojeve
takav da je za sve neparne prirodne brojeve 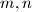 izraz
izraz 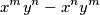 djeljiv s
djeljiv s  .
. takvi da je
takvi da je 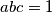 . Dokaži da je
. Dokaži da je 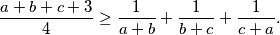
 i
i  sijeku se u točkama
sijeku se u točkama  tako da
tako da  siječe
siječe  i
i  i
i  tako da je
tako da je  . Dokaži da je pravac
. Dokaži da je pravac 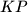 paralelan s težišnicom trokuta
paralelan s težišnicom trokuta 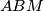 povučenom iz točke
povučenom iz točke