2. ELMO
Neka je  konačan skup točaka u ravnini. Neka je
konačan skup točaka u ravnini. Neka je 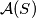 skup pravaca pridruženih skupu
skup pravaca pridruženih skupu  takav da je za svaki
takav da je za svaki 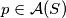 suma kvadrata udaljenosti točaka iz
suma kvadrata udaljenosti točaka iz  od
od  minimalna.
minimalna.
a) Ako je  osnosimetričan s obzirom na pravac
osnosimetričan s obzirom na pravac  i nema točaka na
i nema točaka na  , mora li neki
, mora li neki 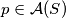 biti osnosimetričan s obzirom na
biti osnosimetričan s obzirom na  ?
?
b) Ako je  centralnosimetričan s obzirom na točku
centralnosimetričan s obzirom na točku  i ne sadrži
i ne sadrži  , mora li svaki
, mora li svaki 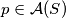 biti centralnosimetričan s obzirom na
biti centralnosimetričan s obzirom na  ?
?
(Borna Šimić)
 Školjka
Školjka  i
i  . Ako je
. Ako je 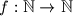 funkcija takva da za svaki
funkcija takva da za svaki 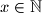 vrijedi
vrijedi 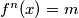 i da za sve različite
i da za sve različite 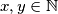 vrijedi
vrijedi 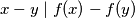 mora li vrijediti
mora li vrijediti 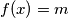 za sve
za sve  ?
?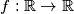 takve da
takve da 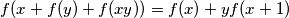 za sve
za sve 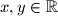 .
. . Neka su
. Neka su 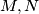 polovišta stranica
polovišta stranica 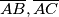 . Neka su
. Neka su 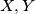 točke na simetralama stranica
točke na simetralama stranica 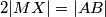 i
i 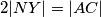 . Neka je
. Neka je  nožište visine iz vrha
nožište visine iz vrha  u trokutu
u trokutu 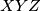 raspolavlja stranicu
raspolavlja stranicu  .
.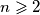 za koje je moguće da svaka
za koje je moguće da svaka  čvora
čvora  zadovoljavaju sljedeće uvjete:
zadovoljavaju sljedeće uvjete: 