1. lakša simulacija državnog natjecanja 2020.
Na ploči je napisano 2020 prirodnih brojeva. Svaku minutu, na ploču dopišemo novi red brojeva na sljedeći način. Ispod svakog broja  u prethodnom redu napišemo broj
u prethodnom redu napišemo broj 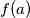 gdje
gdje 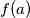 predstavlja broj pojavljivanja broja
predstavlja broj pojavljivanja broja  u prethodnom redu. Dokažite da ćemo u nekom trenutku, jedan za drugim, napisati isti red brojeva.
u prethodnom redu. Dokažite da ćemo u nekom trenutku, jedan za drugim, napisati isti red brojeva.
 Školjka
Školjka 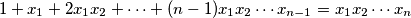 za različite prirodne brojeve
za različite prirodne brojeve 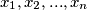 .
.  s ortocentrom
s ortocentrom  . Neka je
. Neka je  polovište stranice
polovište stranice  , a
, a  drugo sjecište pravca
drugo sjecište pravca 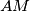 i opisane kružnice
i opisane kružnice  . Neka je
. Neka je  centralno simetrična slika točki
centralno simetrična slika točki 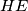 okomit na pravac
okomit na pravac  koji zadovoljavaju relaciju
koji zadovoljavaju relaciju 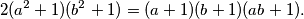
 i
i  se pravokutnik dimenzija
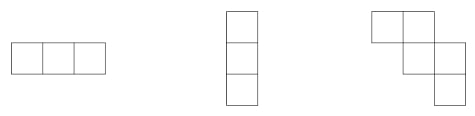
se pravokutnik dimenzija 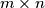 može popločati (bez preklapanja) figurama sastavljenih od jediničnih kvadrata kao na slici?
može popločati (bez preklapanja) figurama sastavljenih od jediničnih kvadrata kao na slici?