Diofantske jednadžbe (lakša grupa)
Teorem 1 (Homogena linearna diofantska jednadžba): Diofantska jednadžba oblika 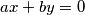 gdje su
gdje su 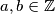 ,
, 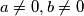 ima beskonačno mnogo cjelobrojnih rješenja, takvih da su
ima beskonačno mnogo cjelobrojnih rješenja, takvih da su 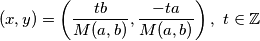
Teorem 2 (Linearna diofantska jednadžba): Diofantska jednadžba oblika 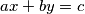 gdje su
gdje su 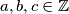 ,
, 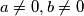 ima cjelobrojna rješenja ako i samo ako
ima cjelobrojna rješenja ako i samo ako 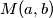 dijeli
dijeli  . Tada ih ima beskonačno mnogo. Također, sva su rješenja oblika zbroja jednog partikularnog i skupa rješenja homogenog.
. Tada ih ima beskonačno mnogo. Također, sva su rješenja oblika zbroja jednog partikularnog i skupa rješenja homogenog.
PRIMJER 1:
Riješimo homogenu diofantsku jednadžbu 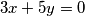 .
.
RJEŠENJE:
Izrazimo jednu nepoznanicu pomoću druge: 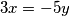 . Budući da je
. Budući da je  cijeli broj,
cijeli broj,  mora biti djeljiv s 3, tj.
mora biti djeljiv s 3, tj.  je oblika
je oblika 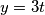 gdje je
gdje je  neki cijeli broj. Iz toga dobivamo da je
neki cijeli broj. Iz toga dobivamo da je 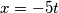 . Dobili smo da su rješenja početne jednadžbe svi uređeni parovi
. Dobili smo da su rješenja početne jednadžbe svi uređeni parovi 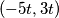 ,
, 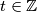 .
.
PRIMJER 2:
Riješimo diofantsku jednadžbu 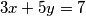 .
.
RJEŠENJE:
Pokušajmo pronaći neki par 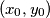 koji zadovoljava jednadžbu. Pogađanjem možemo naći uređen par
koji zadovoljava jednadžbu. Pogađanjem možemo naći uređen par 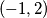 što nam je zapravo jedno partikularno rješenje naše diofantske jednadžbe.
što nam je zapravo jedno partikularno rješenje naše diofantske jednadžbe.
Promatrajmo sada homogenu jednadžbu 3x + 5y = 0. Iz prethodnog primjera znamo da su rješenja te jednadžbe svi uređeni parovi 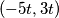 , gdje je
, gdje je 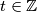 .
.
Iz Teorema 1.3. zaključujemo da su rješenja opće jednadžbe parovi 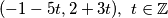 .
.
Zadatci za samostalno rješavanje
1. Riješi homogenu diofantsku jednadžbu: 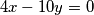 .
.
2. Riješi diofantsku jednadžbu: 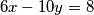 .
.
3. Riješi diofantsku jednadžbu: 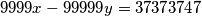 .
.
Lema 1: Umnožak faktora je nula ako i samo ako je barem jedan od faktora nula.
PRIMJER 1:
Riješi diofantsku jednadžbu: 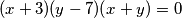 .
.
RJEŠENJE:
Po lemi, vidimo da su rješenja oblika 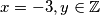 (ako je prva zagrada jednaka nuli),
(ako je prva zagrada jednaka nuli), 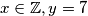 (ako je druga zagrada jednaka nuli) i
(ako je druga zagrada jednaka nuli) i 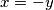 (ako je treća zagrada jednaka nuli; ovo možete zapisati i preko nekog parametra).
(ako je treća zagrada jednaka nuli; ovo možete zapisati i preko nekog parametra).
Nema veze što se neki skupovi rješenja preklapaju, na primjer 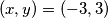 (kada su prva i treća zagrade jednake nuli), bitno je samo da pokrijete sva rješenja.
(kada su prva i treća zagrade jednake nuli), bitno je samo da pokrijete sva rješenja.
PRIMJER 2:
Riješimo diofantsku jednadžbu 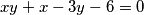 .
.
RJEŠENJE:
Zadana jednadžba zapravo je jednaka: 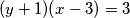 . Dakle, dovoljno je riješiti samo slučajeve kada je jedna zagrada jednaka
. Dakle, dovoljno je riješiti samo slučajeve kada je jedna zagrada jednaka 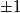 , a druga
, a druga 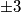 . Sada izjednačavamo zagrade s tim vrijednostima. Konkretno, rješenja su
. Sada izjednačavamo zagrade s tim vrijednostima. Konkretno, rješenja su 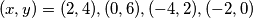 .
.
Zadatci za samostalno rješavanje
1. Riješi u cijelim brojevima: 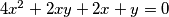 .
.
2. Riješi u cijelim brojevima: 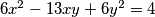 .
.
3. Nađi sva cijelobrojna rješenja za: 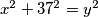 .
.
Cilj metode kvocijenata je izraziti jednu nepoznanicu u potpunosti preko druge, i onda komentirati slučajeve kada je izraz cijeli broj.
Lema 1(Zatvorenost na zbrajanje i oduzimanje): Skup cijelih brojeva zatvoren je i s obzirom na zbrajanje i oduzimanje, tj. ukoliko cijelom broju oduzmemo ili pribrojimo drugi cijeli broj, rezultat će i dalje biti cijeli broj. Specijalan slučaj ovoga je: 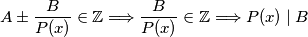
PRIMJER 1:
Riješi diofantsku jednadžbu 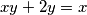 .
.
RJEŠENJE:
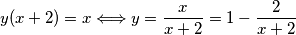 . Sada vidimo da je
. Sada vidimo da je 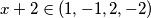 jer mora biti djelitelj od 2 kako bi razlomak bio cjelobrojan, pa je
jer mora biti djelitelj od 2 kako bi razlomak bio cjelobrojan, pa je 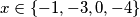 i (daljnjim uvrštavanjem)
i (daljnjim uvrštavanjem) 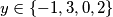 .
.
PRIMJER 2:
Riješi diofantsku jednadžbu: 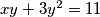
RJEŠENJE:
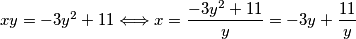 pa je
pa je 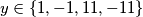 , što daje rješenja redom
, što daje rješenja redom 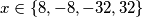 .
.
Zadatci za samostalno rješavanje
1. (Školsko 2019. SŠ1 5.) Odredi sve parove 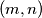 cijelih brojeva za koje vrijedi
cijelih brojeva za koje vrijedi 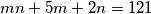
2 (Državno 1998. SŠ1 2.) Nađite sve prirodne brojeve  i
i  koji zadovoljavaju jednadžbu:
koji zadovoljavaju jednadžbu: 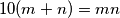
Metoda posljednje znamenke je samo poseban slučaj metode kongruencija kojom ćemo se pozabaviti neki drugi put koristeći kao uvod predavanje s ovogodišnje Ljetne škole: https://drive.google.com/drive/folders/170lvUaNcIh_BsNTtRsrZHARXhKRW2-4t?usp=sharing
PRIMJER 1:
Riješi diofantsku jednadžbu 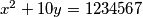 .
.
RJEŠENJE:
Kvadrat cijelog broja može završavati jednom od znamenaka 0, 1, 4, 5, 6 ili 9. S obzirom da 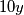 završava znamenkom 0, zadnja znamenka od
završava znamenkom 0, zadnja znamenka od 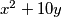 može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
PRIMJER 2:
Riješimo diofantsku jednadžbu 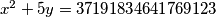 .
.
RJEŠENJE:
Budući da kvadrat cijelog broja završava sa znamenkom 0, 1, 4, 5, 6, ili 9,a broj 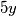 sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
Zadatci za samostalno rješavanje
1. Nađi sve parove prirodnih brojeva 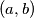 takvih da vrijedi:
takvih da vrijedi: 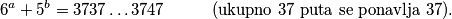
2. Nađite cjelobrojna rješenja jednadžbe: 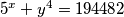 .
.
U metodi nejednakosti, želimo ograničiti broj mogućnosti tako da najprije ograničimo neku nepoznanicu pomoću nejednakosti. Zatim nam ostaje relativno malo primjera koje možemo provjeriti ručno i vidjeti ima li rješenja.
PRIMJER:
U skupu prirodnih brojeva riješite jednadžbu 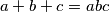 .
.
RJEŠENJE:
Pošto je jednadžba potpuno simetrična, bez smanjenja općenitosti neka je 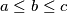 . Tada je
. Tada je 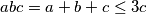 , odnosno
, odnosno 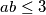 (kako je
(kako je 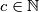 , smijemo nejednakost podijeliti s
, smijemo nejednakost podijeliti s  ) , pa razlikujemo tri slučaja:
) , pa razlikujemo tri slučaja:  Dakle, jedino rješenje je
Dakle, jedino rješenje je 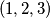 i sve permutacije tog skupa.
i sve permutacije tog skupa.
PRIMJER:
Dokažite da izraz 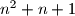 , gdje je
, gdje je  , ne može biti kvadrat cijelog broja.
, ne može biti kvadrat cijelog broja.
RJEŠENJE:
Metoda koju ćemo primijeniti poznata je i kao smještanje među kvadrate, tj. pokazujemo da broj ne može biti kvadrat tako da ga smjestimo između dva uzastopna kvadrata.
Primijetimo da zbog  tj.
tj. 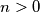 vrijedi
vrijedi 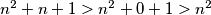 . S druge strane, slično zaključujemo i
. S druge strane, slično zaključujemo i 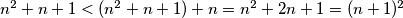 . No kako su
. No kako su  i
i 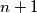 su 2 uzastopna prirodna broja, a
su 2 uzastopna prirodna broja, a 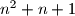 strogo između njihovih kvadrata, taj broj nikako ne može biti kvadrat nekog prirodnog broj.
strogo između njihovih kvadrata, taj broj nikako ne može biti kvadrat nekog prirodnog broj.
Zadatci za samostalno rješavanje
1. (Općinsko 2010. SŠ4 4.) Odredi sve parove prirodnih brojeva 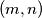 takvih da vrijedi
takvih da vrijedi 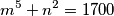 .
.
2. (Županijsko 2018. SŠ1 2.) Odredi sve parove cijelih brojeva 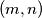 takve da je:
takve da je: 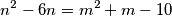
 Školjka
Školjka