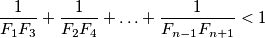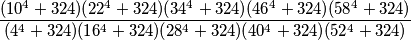Teleskopiranje (teža grupa)
U ovom predavanju otkrit ćete kako pronaći "formule" po kojim se zbrajaju razni nizovi koji u nazivniku (a možda i brojniku) ovise o svojem indeksu (položaju u nizu).
Teleskopiranje je matematička metoda rješavanja algebarskih zadataka kojom se složeniji razlomci rastavljaju na jednostavnije razlomke (koji se tada u većini slučajeva skrate).
Lema (Rastav na linearne komponente) Svaki složeni razlomak može se rastaviti na linearne komponente. 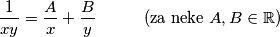
Primijetimo da lemu možemo prošiti induktivno i na razlomke s više komponenata u nazivniku (pa onda svaku možemo rastaviti). Također, nije nužno da je broj 1 u brojniku (onda možemo obje strane pomnožiti s nekim izrazom).
PRIMJER 1: Odredi zbroj: 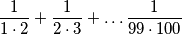 .
.
RJEŠENJE:
Zapišimo neki općeniti član tog niza: 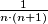 . Taj razlomak želimo rastaviti na neke razlomke
. Taj razlomak želimo rastaviti na neke razlomke 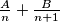 . Rješavanjem sustava jednadžbi za konkretne vrijednosti
. Rješavanjem sustava jednadžbi za konkretne vrijednosti  (npr.
(npr.  i
i  ) dobivamo
) dobivamo 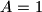 ,
, 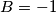 . Sada samo trebamo izračunati zbroj:
. Sada samo trebamo izračunati zbroj: 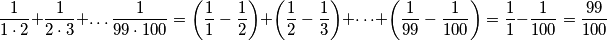
PRIMJER 2: Neka je  takav da je
takav da je 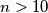 . Izračunaj sljedeći umnožak:
. Izračunaj sljedeći umnožak: 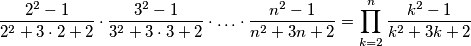
RJEŠENJE:
Primijetimo da za svaki  vrijedi
vrijedi 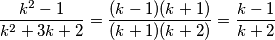 Sada je naš umnožak jednak
Sada je naš umnožak jednak 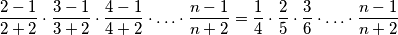 Primijetimo da će se pokratiti svi brojnici i nazivnici koji su veći od
Primijetimo da će se pokratiti svi brojnici i nazivnici koji su veći od  i manji od
i manji od  , tako da ostaje
, tako da ostaje 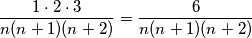
OPREZ: Uvjet 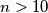 nam je trebao da ne bismo imali preklapanja brojeva koji se nisu pokratili.
nam je trebao da ne bismo imali preklapanja brojeva koji se nisu pokratili.
Na primjer, za 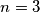 ne postoje brojnici niti nazivnici koji su veći od
ne postoje brojnici niti nazivnici koji su veći od  i manji od
i manji od  , pa
, pa
treba zasebno argumentirati takav slučaj.
 Školjka
Školjka 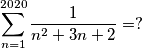
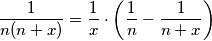
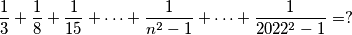
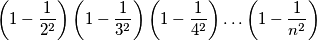
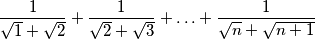
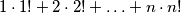
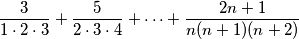
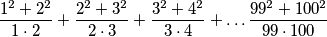
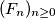 Fibonaccijevi brojevi, odnosno
Fibonaccijevi brojevi, odnosno 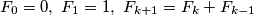 za svaki prirodan broj
za svaki prirodan broj  . Neka je
. Neka je