Državno natjecanje 1996 SŠ2 1
Dodao/la:
arhiva1. travnja 2012. Ako funkcija

zadovoljava uvjete
a)
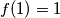
b)
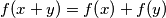
,
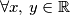
c)
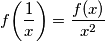
,
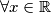
,
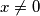
koliko je
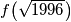
?
%V0
Ako funkcija $f$ zadovoljava uvjete
a) $f\!\left(1\right) = 1$
b) $f\!\left(x+y\right) = f\!\left(x\right) + f\!\left(y\right)$, $\forall x,\,y \in \mathbb{R}$
c) $\displaystyle f\!\left(\frac1x\right) = \frac{f\!\left(x\right)}{x^2}$, $\forall x \in \mathbb{R}$, $x \neq 0$
koliko je $f\!\left(\sqrt{1996}\right)$?
Izvor: Državno natjecanje iz matematike 1996